練習問題解答(クワイン・マクラスキー法)
山本昌志1
Date: 2003年10月27日
- 問題1
- 4変数の真理値表で、
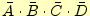 、
、
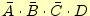 、
、
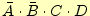 、
、
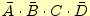 、
、
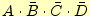 、
、
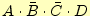 、
、
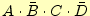 が1のときの論理式を
クワイン・マクラスキー法で簡単化せよ。
が1のときの論理式を
クワイン・マクラスキー法で簡単化せよ。
- 解答
- ちょっと問題の表現がへんですが、教科書にそう書いてあるの
で良しとしましょう。この問題は、4論理変数
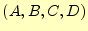 の値が
の値が
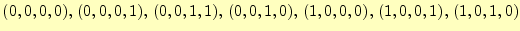 のとき、論理関数
のとき、論理関数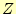 の値
が1になっていると言っていると解釈します。この場合のクワイ
ン・マクラスキー法の圧縮表を図1に示
します。これから、主項図を作成すると、表
の値
が1になっていると言っていると解釈します。この場合のクワイ
ン・マクラスキー法の圧縮表を図1に示
します。これから、主項図を作成すると、表![[*]](crossref.png) のようになります。この主項図から、最も簡単な論理関数
は、
のようになります。この主項図から、最も簡単な論理関数
は、
となります。
表 1:
問題1の主項図
| <#236#> |
最小項 |
| |
0000 |
0001 |
0010 |
1000 |
0011 |
1001 |
| 00__ |
◎ |
◎ |
◎ |
|
◎ |
|
|
| _00_ |
◎ |
◎ |
|
◎ |
|
◎ |
|
| _0_0 |
◎ |
|
◎ |
◎ |
|
|
◎ |
- 問題2
- 以下の論理関数をクワイン・マクラスキー法で簡単にせよ。
- 解答
- この論理関数の圧縮表は、図2のように
なります。これから、主項図を作成すると、表
![[*]](crossref.png) のようになります。この主項図から、最も簡単な論理関数
は、
のようになります。この主項図から、最も簡単な論理関数
は、
となります。
表 2:
問題2の主項図
| <#275#> |
最小項 |
| |
0001 |
0100 |
1000 |
0011 |
0110 |
1001 |
1010 |
1011 |
| 01_0 |
|
◎ |
|
|
◎ |
|
|
|
|
| _110 |
|
|
|
|
○ |
|
|
|
○ |
| 1_10 |
|
|
|
|
|
|
○ |
|
○ |
| _0_1 |
◎ |
|
|
◎ |
|
◎ |
|
◎ |
|
| 10__ |
|
|
◎ |
|
|
◎ |
◎ |
◎ |
|
図 1:
クワイン・マクラスキー法の圧縮表(問題1)
|
|
図 2:
クワイン・マクラスキー法の圧縮表(問題2)
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
![[*]](crossref.png) のようになります。この主項図から、最も簡単な論理関数
は、
のようになります。この主項図から、最も簡単な論理関数
は、
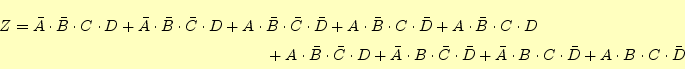
![[*]](crossref.png) のようになります。この主項図から、最も簡単な論理関数
は、
のようになります。この主項図から、最も簡単な論理関数
は、