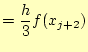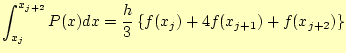3 シンプソンの公式
台形公式の考え方は簡単であるが、精度はあまりよくない。そこで、よく似た考え方で精 度が良いシンプソンの公式を説明する。台形公式は、分割点の値を一次関数(直線)で近似 を行い積分を行った。要するに折れ線近似である。ここで、1次関数ではなく、高次の関 数で近似を行えばより精度が上がることは、直感的に分かる。
2次関数で近似を行うことを考える。2次関数で近似するためには、3点必要である。3つの
分点をそれぞれ、
![]() とする。そして、この2次関数を
とする。そして、この2次関数を![]() と
する。
と
する。![]() はラグランジュ補間に他ならないので、
はラグランジュ補間に他ならないので、
となる。図3に示すとおりである。
これを、区間
![]() で積分する。紙面の都合上、式
(11)の右辺を各項毎に積分を行う。まず、右辺第1項で
あるが、それは以下のようになる。
で積分する。紙面の都合上、式
(11)の右辺を各項毎に積分を行う。まず、右辺第1項で
あるが、それは以下のようになる。
同様に、第2,3項を計算すると
となる。以上より、近似した2次関数
となる。
これは、ある区間
![]() の積分で、その巾は
の積分で、その巾は![]() である。区間
である。区間![]() にわ
たっての積分
にわ
たっての積分![]() は、式(15)を足し合わせればよい。ただし、
は、式(15)を足し合わせればよい。ただし、
![]() と足し合わせる。
と足し合わせる。
 |
これが、シンプソンの公式と呼ばれるもので、先ほどの台形公式よりも精度が良い。精度 は、
この式から、分割数![]() は偶数でなくてはならないことがわかる。これに注意して、プロ
グラムを作成しよう。
は偶数でなくてはならないことがわかる。これに注意して、プロ
グラムを作成しよう。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年1月25日
![\includegraphics[keepaspectratio, scale=1.0]{figure/simpson.eps}](img24.png)
![\begin{equation*}
% latex2html id marker 842
\begin{aligned}\text{式(\ref{eq:sim...
...i^2}{2}+2h^2\xi\right]_0^{2h} &=\frac{h}{3}f(x_j) \end{aligned}\end{equation*}](img26.png)