1 はじめに
以前、常微分方程式の数値計算について学習した。独立変数が1個のものを常微分方程式、 2個以上のものを偏微分方程式と言うのは数学の授業で学んだとおりである。実際、自然 現象は常微分方程式よりも、偏微分方程式で記述されることが多い。常微分方程式が役に 立たないと言っているのではなく、より広範囲には偏微分方程式が使われているというこ とである。自然界が、ここでは、偏微分方程式、特にラプラス方程式を差分法というテクニックで数 値計算する方法を学習する。偏微分方程式は、いろいろなものがあるが、最初 に学習する分には、意味がわかりやすい方程式と言うことで、これを教 材に選んだ。実際には、図1の静電磁場や、図 2の熱の問題に、この方程式は表れる。
- 図1は、紙面と垂直方向に無限に長い正方形の金属筒に、電線 が2本通っている。正方形の筒は0Vにアースされており、2本の電線はそれぞれ、 30Vと-20Vである。この状態で、筒内部のポテンシャル(電圧)の分布を求めなさい という問題である。
- 図2は、紙面方向に非常に長い豆腐があり、その周りは0 ℃の水で満たされている。そして、その豆腐に30℃と-20℃の金属棒が突き刺 さっている状況である。豆腐内部の温度分布を求めなさいというのが問題であ る。
これらは、物理的には異なる問題であるが、ポテンシャルや温度が満たす方程式は同じで ある。方程式が同じならば解は同じで、同じ計算手法が使えることを理解して欲しい。こ れらが満たすのはラプラス方程式
| (1) |
と言われるものである。
と2次元問題になる。ここではこの偏微分方程式の近似解を数値計算により求めるのが目 的である。ここでの学習を通して、プログラムが完成すると、図3のよ うな解のグラフを求めることができる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年2月8日
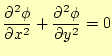
![\includegraphics[keepaspectratio, scale=0.8]{figure/potential.eps}](img6.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/temperature.eps}](img7.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/solution.eps}](img8.png)