5 進行波の取り扱い

先の練習問題、弦を三角形に張った後の様子は、定在波である。ここでは、進行波の記述 方法について、コメントしておく。進行波を数値計算すると面白いのでその方法を示す。 進行波を記述するためには、初期条件さえ記述すれば、後の差分方程式は同じである。そ の初期条件の記述の仕方を示す。

元の波動方程式

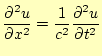$$\frac{\partial^2 u}{\partial x^2}= \frac{1}{c^2}\frac{\partial^2 u}{\partial t^2}$$ (20)

には、明らかに、ダランベールの解

$$u(x,t)=f(x-ct)+g(x+ct)$$ (21)

というものがある。これは元の波動方程式に代入すれば、それを満足していることは直ち に理解できる。ここで、$f(x-ct)$はx軸を正の方向に進む進行波(forward wave)で、 $g(x+ct)$は負の方向に進む後進波(backward wave)である。

初期条件

$$u(x,0)=\phi(x)$$ (22)

の波がx軸を正の方向に進む進行波として取り扱うには、どうしたらよいだろうか?。のこ る条件は、

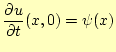$$\frac{\partial u}{\partial t}(x,0)=\psi(x)$$ (23)

である。進行波になるように、$\psi (x)$を決めればよい。$u(x,t)$を進行波と仮定する と、式(22)から

$$u(x,\Delta t)=\phi(x-c\Delta t)$$ (24)

となる。この式を使って、$\psi (x)$を求めることにする。$\psi (x)$の定義より、

$$\begin{aligned}\psi(x) &=\frac{\partial u}{\partial t}(x,0) &... ...-\phi(x-\Delta x)}{\Delta x} &=-c\frac{d\phi}{dx} \end{aligned}$$

となる。進行波にするためには、$\psi (x)$は$\phi(x)$の導関数ににすればよいのである。

念のため言っておくが、後進波にするためには

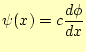$$\psi(x)=c\frac{d\phi}{dx}$$ (26)

とすればよい。
ホームページ: Yamamoto's laboratory
著者: 山本昌志