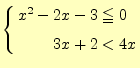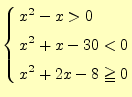少し,役に立つ数学の問題を解くプログラムの作成を行う.絶対にここのプログラムの内
容を理解せよ.これが理解できないと,今後の授業で大変困ることになる.
- [練習1]
- 関数
| |
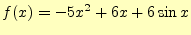 |
|
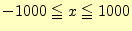 |
|
(1) |
の最大値を計算するプログラムを作成せよ.計算のステップ幅--計算精
度を表す--を
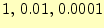 と変化させて計算させてみよ.ス
テップ幅が
と変化させて計算させてみよ.ス
テップ幅が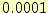 のとき,コンピューターの計算回数はどの程度で
あろうか.
のとき,コンピューターの計算回数はどの程度で
あろうか.
- [練習2]
- 基礎数学の教科書p.62の練習問題2-Aの2.(2)の連立不等式
| |
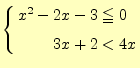 |
|
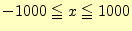 |
|
(2) |
を計算するプログラムを作成せよ.計算のステップ幅--計算精度を表す--
は,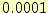 とせよ.
とせよ.
- [練習3]
- 関数
| |
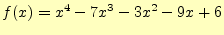 |
|
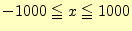 |
|
(3) |
の最小値を計算するプログラムを作成せよ.計算のステップ幅は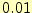 と
せよ.
と
せよ.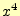 は教科書のp.127に示しているようにpow(x,4)と数
学関数を使うこともできるが,通常は,
は教科書のp.127に示しているようにpow(x,4)と数
学関数を使うこともできるが,通常は,
と展開して,最後の式をプログラムに書き込む.この方が,
pow()関数を使うより,コンピューターの計算が早い.嘘だと思
うなら,比較してみよ.
- [練習4]
- 基礎数学の教科書p.63の練習問題2-Bの1.(2)の連立不等式
| |
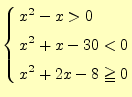 |
|
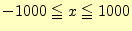 |
|
(5) |
を計算するプログラムを作成せよ.計算のステップ幅--計算精度を表す--
は,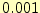 とせよ.
とせよ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成18年9月20日