4 完全直交系
ある任意の関数| (11) | ||
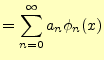 |
(12) |
そして,関数同志の積の積分で,
 |
(13) |
の場合,直行系と言う.積分の範囲は関数の定義域である.特に,
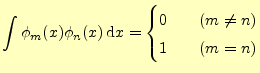 |
(14) |
の場合,規格化直行系2と呼ぶ.これら, 完全系や直交系の話は,ベクトルを他のベクトル列の和で表すのと似ていることに注意せ よ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年12月1日
| (11) | ||
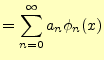 |
(12) |
 |
(13) |
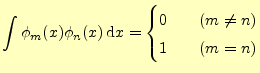 |
(14) |