7 課題
- [問1]
- 正三角形はどのような対称性があるか
- [問2]
- 円柱はどのような対称性があるか
- [問3]
- 球はどのような対称性があるか
- [問4]
- 運動方程式が
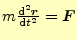 の場合,平行移動に対して対称である.実際とは異なるが,平行移動に対して対称でない運動方程式を作ってみよ.
の場合,平行移動に対して対称である.実際とは異なるが,平行移動に対して対称でない運動方程式を作ってみよ.
- [問5]
- 2つのベクトル
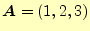
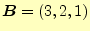
の と
と
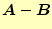 を示せ.
を示せ.
- [問6]
- 前問のベクトル
 と
と
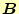 の大きさを示せ.
の大きさを示せ.
- [問7]
- 2つの位置ベクトル
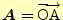 ,
,
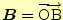 の終点
の終点
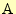 と
と
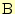 の間を
の間を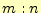 の比に分ける点
の比に分ける点
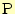 の位
置ベクトルを
の位
置ベクトルを
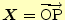 とすれ
ば,
とすれ
ば,
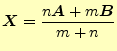
であることを示せ. - [問8]
- 三角形
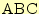 の重心を
の重心を
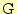 とし,点
とし,点
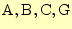 の位置ベクトル
をそれぞれ,
の位置ベクトル
をそれぞれ,
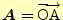 ,
,
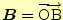 ,
,
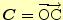 ,
,
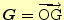 とすれば,
とすれば,
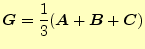
であることを示せ. - [問9]
- 3つの互いに垂直な平面鏡からなる反射鏡(コーナーキュウブ)がある.この反射鏡 に入った光線(3つの反射鏡で反射される)は,入射方向と平行 な方向にでていくことを示せ.これは,自転車の反射板の原理 である.アポロ宇宙船が月面にコーナーキューブを置いて,地 球からのレーザー光を反射させたこともあった.これにより地 球との距離を計った.(ヒント:入射光線をベクトルの 成分で表現する.そして,反射鏡はカーテシアン座標系のxy, yz, zx平面にあるとする.)
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年5月26日