5 練習問題

[練習1]

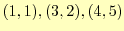3点 $(1,1),(3,2),(4,5)$ を通る曲線をラグランジュ補間して，区間 $[-1,5]$ のグラフを書け．

[練習2]

以下のようなデータが得られた．

x	-1.0	-0.9	-0.8	-0.7	-0.6	-0.5	-0.4	-0.3	-0.2	-0.1	0.0
y	0.038	0.047	0.058	0.075	0.100	0.137	0.200	0.307	0.500	0.800	1.000

x	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
y	0.800	0.500	0.307	0.200	0.137	0.100	0.075	0.058	0.047	0.038

このデータは，関数 $y=1/(1+25x^2)$ の値である．21個の点があるが， ここでは補間をするデータの個数と補間のグラフの関係を調べる．

• 等間隔の6個のデータ，すなわち

  $$x=-1.0,\,-0.6,\,-0.2,\,0.2,\,0.6,\,1.0$$

  
  
  の場合のラグランジュ補間の結果をグラフに示せ．
• 等間隔の11個のデータ，すなわち

  $$x=-1.0,\,-0.8,\,-0.6,\,-0.4,\,-0.2,\,0.0,\,0.2,\,0.4,\,0.6,\,0.8,\,1.0$$

  
  
  の場合のラグランジュ補間の結果をグラフに示せ．
• 全てのデータを用いた場合のラグランジュ補間の結果をグラフに示せ．

以上の結果から，補間の点数が増加した場合，ラグランジュ補間で はどのようなことが起きるか?-考察せよ．

[練習3]

先の[練習2]と同じことをスプライン補間で行え．

[練習4]

WEBにデータを掲載する．それを二次関数で最小二乗近似せよ．

ホームページ: Yamamoto's laboratory
著者: 山本昌志