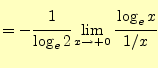エントロピーの計算では,
 |
(21) |
の関数がしばしば表れる.情報科学の分野では,変数 の部分には確率になることが多
い.そのため,
の部分には確率になることが多
い.そのため,![$ [0,1]$](img212.png) の間で,この関数の形を覚えておくと良いだろう.この関数をプ
ロットすると,図7のようになうる.
の間で,この関数の形を覚えておくと良いだろう.この関数をプ
ロットすると,図7のようになうる.
図:
 の関数の形.
の関数の形.
|
|
ここで,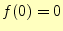 なのか?--という疑問が湧く.
なのか?--という疑問が湧く.
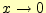 の極限では,
の極限では,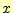 はゼ
ロに近づくが,
はゼ
ロに近づくが, は
は となる.
となる. の部分をちゃんと調べなくてはなら
ない.そこで,
の部分をちゃんと調べなくてはなら
ない.そこで, の極限の値を調べてみることにする.
の極限の値を調べてみることにする.
 |
(22) |
この手に極限の問題は,ロピタルの定理を使う.
これで,めでたしめでたしである.この関数では, は不定になるであろう.
は不定になるであろう. のところではかなり特異な性質がある.ただし,
のところではかなり特異な性質がある.ただし,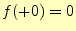 となる.
となる.
それでは,質問.
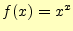
とする.
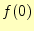
はどうなるか?
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年12月7日
![]() なのか?--という疑問が湧く.
なのか?--という疑問が湧く.
![]() の極限では,
の極限では,![]() はゼ
ロに近づくが,
はゼ
ロに近づくが,![]() は
は![]() となる.
となる.![]() の部分をちゃんと調べなくてはなら
ない.そこで,
の部分をちゃんと調べなくてはなら
ない.そこで,![]() の極限の値を調べてみることにする.
の極限の値を調べてみることにする.