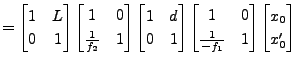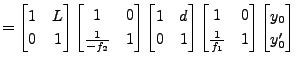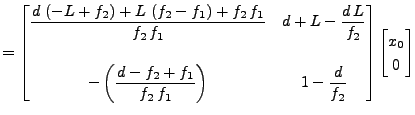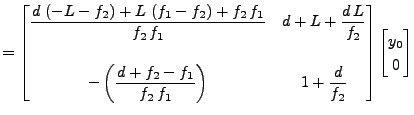: トリプレット
: Q-magnetによるビーム収束
: Q-magnetによるビーム収束
x方向とy方向それぞれに収束力を持つQ-magnetを並べたものをダブレットという。
今、magnet間の距離がdとして、ビームが距離Lだけ進んだときの位相空間の式は次のようになる。
さて、この式より収束の条件を求める。
平行ビームを入射しx,y方向が同時ににビーム系が0の点が存在すればよい。
つまり、
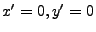 とし、
とし、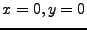 となればよい。
では実際に
となればよい。
では実際に
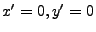 として式(3), (4)を計算してみると、
として式(3), (4)を計算してみると、
となる。
これより、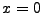 となる距離
となる距離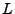 を求めると、
を求めると、
となり、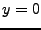 となる
となる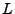 は
は
である。つまりxy方向の収束の条件は、
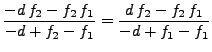 |
(9) |
であり、これを整理すると、
となる。
natsui takuya
平成19年2月9日