2 Mathematcaのフーリエ変換
マニュアル [2]から、Mathematicaのフーリエ変換の定義を調べる。それ によると、デフォルトの設定の場合の離散フーリエ変換と逆離散フーリエ変換は |
(26) | |||
 |
(27) |
となっている。ここで、
1節で示した離散フーリエ変換は、![]() 個のデータの並び
が、
個のデータの並び
が、
![]() のように0から始まっていた。それに対して、
Mathematicaの場合は、
のように0から始まっていた。それに対して、
Mathematicaの場合は、![]() から始まるっている。Mathematicaのフーリエ変換を調べるた
めに、その並びを0から数え始めること
から始まるっている。Mathematicaのフーリエ変換を調べるた
めに、その並びを0から数え始めること
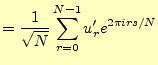 |
(28) | |||
 |
(29) |
となる。こうなると、式(24)や(25)とほとんど同じ であることが分かる。前節とMathematicaのフーリエ変換で異なる部分は、
- 前節の結果では、和の前の係数が
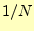 や
や 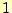 になっている。それに対して、
Mathematicaでは
になっている。それに対して、
Mathematicaでは
 となっている。
となっている。
- 指数関数の符号が前節とMathematicaで異なる。
 |
(30) |
としているためでる。本質的な違いはなにもない。
以上をまとめると、Mathematicaの離散フーリエ変換は、次のようになる。
- 離散フーリエ変換の結果の
 は、
は、
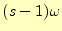 の角振動数の振幅を表す。
の角振動数の振幅を表す。
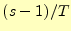 の振動数の振幅と言っても良い。
の振動数の振幅と言っても良い。
- 逆離散フーリエ変換の結果の
 は、
は、
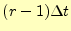 の時の値を表す。
の時の値を表す。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月29日