3 戻り値がある関数

次に示す例は、2倍角の公式

$$\sin 2\theta=2\sin\theta\cos\theta$$ (1)

を確認するプログラムである。角度を0〜360度まで、1度ずつ変化させてそれぞれを、表 示させている。

	#include <stdio.h>
	#include <math.h>

	double function1(double x);
	double function2(double x);

	/*==============================================================*/
	/*   main function                                              */
	/*==============================================================*/
	int main(void){
	  int kakudo;
	  double pi, theta, y1, y2;

	  pi=3.141592;

	  for(kakudo=0; kakudo<=360; kakudo++){
	    theta = kakudo*pi/180.0;
	    y1 = function1(theta);
	    y2 = function2(theta);
	    printf("%d\t%lf\t%lf\n", kakudo, y1, y2);
	  }

	  return 0;
	}
	

	/* <<<<<<<<<< これ以降は、サブルーチン >>>>>>>>>>>>>>>>>>>>>>>>>>>>*/

	/*==============================================================*/
	/*   sin(2x)の計算                                              */
	/*==============================================================*/
	double function1(double x){
	  double y;

	  y=sin(2.0*x);

	  return y;
	}


	/*==============================================================*/
	/*   sin(x)cos(x)の計算                                          */
	/*==============================================================*/
	double function2(double x){
	  double y;
  
	  y=2.0*sin(x)*cos(x);

	  return y;
	}

このプログラムをコンパイルする場合、以下のようなオプションを付ける必要がある。こ れは、数学関数sin()を使っているためである。

	cc -lm -o bai baikaku1.c

オプション-lmが数学関数を使いますよとコンパイラーに知らせているのである。実 際には、数学のライブラリーも併せてコンパイルしているのである。この辺のことは気に しないで、数学関数を使う場合、このプログラムの2行目に書いてある#include <math.h>とあわせて、使うと憶えれば良 い。

3.1 練習問題

以下の練習問題のプログラムを作成すること。

3.1.1 2倍角の公式(その2)

もう一つの2倍角の公式

$$\cos 2\theta=\cos^2\theta-\sin^2\theta$$ (2)

を確認するプログラムを作成せよ。

• ただし、例にならって、プログラムを作成すること。。
• 公式が成り立っていることをよく確認すること。

3.1.2 三角形の面積

三角形の面積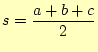$S$をヘロンの公式

$$s=\frac{a+b+c}{2}$$ (3)

$$S=\sqrt{s(s-a)(s-b)(s-c)}$$ (4)

を使って計算するプログラムを作成せよ。ここで、$a,b,c$は辺の長さである。プログラ ムの条件は以下の通りとする。

• キーボードから、辺の長さを読み込む。
• 面積の計算は、関数を使うこと。ただし、 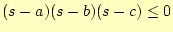$(s-a)(s-b)(s-c)\le 0$の場合は、"三 角形になりません"と表示して、プログラムを止めること。

このプログラムができたならば、再度計算するか否かのメッセージを出す。そして、次の三角形の 面積を計算する、あるいはプログラムを止めるように改造すること。

ホームページ: Yamamoto's laboratory
著者: 山本昌志