4 乗除算はどうするの?

ここで、賢明な諸君は、4則演算の残りの2つ、乗除算はどうしたのという疑問が湧くはずである。湧いて欲しい。

最近のCPUは、これら乗除算のハードウェアーが実装されており、それに対応する機械語命令がある。しかし、単純なCOMET IIには、そのハードウェアはなく、当然機械語命令も無い。そのため、ソフトウェアーでその仕組みを実現させなくてはならない。詳細については、後で学習するが、ちょっとだけ方法を示す。興味深い方法である。

4.1 乗算

4.1.1 算術加算を使う方法

例えば、10×3を計算する場合、10+10+10のように必要な回数だけ足し合わせて乗算を行う。このように算術加算を用いて乗算を行うことができる。ただし、この方法はもっとも原始的で効率の悪い方法である。人間がこの計算を行うのは非現実的であるが、単純作業を非常に高速で行うコンピューター向きの方法である。

この例でもわかるように加算ができれば、乗算はできるのである。

4.1.2 ビットシフトを使う方法

もう少し効率の良い方法は、ビットシフトを使う方法である。これは、小学生のときに学習をした筆算を用いた掛け算と同じである。たとえば、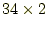 $34\times24$ を計算する場合、筆算は $34\times(2\times10^{1}+4\times10^{0})$ と分解したはずである。そうして、次の手順でこの除算を行ったはずである。

$34\times2$ を計算し、1桁ずらす(10倍する)。
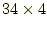$34\times4$ を計算する。
先の計算結果を合計する。この合計816が 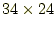$34\times24$ の計算結果である。

同じことを2進数で行う。これがコンピューターによる乗算である。先ほどと同じ計算( $32\times24$ )を行う。これを2進数で表現すると、

$\displaystyle (100010)_2\times(11000)_2=(100010)_2\times(1\times2^4+1\times2^3)$

となる。これを先ほど同様の手順で計算する。

掛け算は1倍なので計算する必要が無く、最初に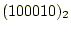を4桁左にずらす(ビットシフト)。すると、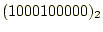となる。
次に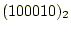を3桁左にずらす。すると、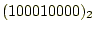となる。
先の計算結果を合計すると、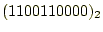となる。これは、10進数の816である。

ここでは、ビットシフトと加算命令を使った。これらの命令が用意されていれば乗算ができることがわかるであろう。実際、CASL IIにはビットシフトの命令は用意されている。

4.2 除算

4.2.1 算術減算を使う方法

の計算は10からから3を引いていきます。そして、負になったら計算は完了です。すると、商と余りが分かります。算術減算を用いて乗除算が出来ます。この例でもわかるように減算ができれば、除算はできるのである。この方法は効率が悪いので、もう少しましな方法を考える。小学生の時に学習した筆算のアルゴリズムを適用すれば効率は良くなる。計算は次のようにする。計算の準備として、10と3を2進数で表す。

$\displaystyle (10)_{10}=(1010)_{2}\qquad\qquad(3)_{10}=(11)_2$

次に示すように計算すれば、計算効率は上がるであろう。計算順序は、筆算での割り算と同じである。

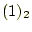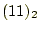からを減算したいが、負になるのでそれは不可とする。
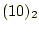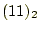からを減算したいが、これも負になるので不可とする。
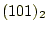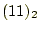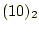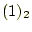からを減算する。それは可能で、結果はで、その桁にが立つ。
先ほどの残りと次の桁を合わせた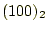は減算可能である。減算の結果は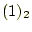で、その桁に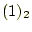が立つ。
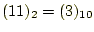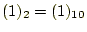これ以上桁がないので、計算は完了である。商は $(11)_2=(3)_{10}$ 余りは $(1)_2=(1)_{10}$ となる。

4.2.2 ビットシフトを使う方法

直ちに、ビットシフトが適用できるのは、割る数が

になっている場合である。ただ、先ほどの筆算のアルゴリズムでもビットシフトは使ってはいる。

ということで、加算と減算ができれば乗除算は可能である。さらに賢明な諸君は、次の疑問が湧くはずである。湧いて欲しい。三角関数や指数関数などは、どうやって計算しているのか?。三角関数や指数関数は、テイラー展開(マクローリン展開)を使うと4則演算に分解できることを学習したはずである。したがって、4則演算ができれば、それらの関数は計算可能である。高級言語のコンパイラーは、これらの関数を4則演算に変換して計算するようにしている。
ホームページ: Yamamoto's laboratory
著者: 山本昌志

Yamamoto Masashi
平成16年9月7日