2 論理加算・減算

論理加算と減算は、データを16ビットの符号なし整数として計算する。前回学習した算術 加算(ADDA)と算術減算(SUBA)は、符号付き整数² として取り扱う。これらの違いに注意が必要 である。たとえば、同じ16ビットのデータでも、10進数の整数として取り扱うとき、次に ようになる。なぜこのようになるか、忘れた者は以前のノートを見よ。

表 1: 符号有り整数と負号無し整数

ビットパターン	符号無整数	符号有整数
0000000001010011	(83)$_{10}$	(83)$_{10}$
1000000001010011	(32851)$_{10}$	(-32685)$_{10}$

2.1 論理加算(ADDL)

2.1.1 内容

命令語	ADDL: ADD Logical (add:加える logical:論理的な)
役割	符号無し整数の足し算を行う命令。
書式	教科書(p.48)の通り。
機能	教科書(p.48)の通り。
フラグレジスタ	教科書(p.49)の通り。

符号無し整数の演算を行うということは、全て正として取り扱う。それなのに、フラグレ ジスタのSFが1になることに対して、疑問に思うだろう。それについては、教科書の 例題で説明する。

2.1.2 使用例

      ADDL  GR0,GR1      ;GR0←GR0+GR1
      ADDL  GR0,A        ;GR0←GR0+(アドレスAの内容)
      ADDL  GR0,A,GR1    ;GR0←GR0+(アドレス[A+GR1]の内容)
      ADDL  GR0,=5       ;GR0←GR0+5

教科書の例題を実行したときのメモリーとレジスターの内容を表 2示す。それらの値は、各行の実行の終了時点での値である。た だし、アスタリスク($\ast$)の箇所は、未定であることを示す。物理的にそれらが存在す るので、値は未定ではあるが、ビットパターンはある。1, 6, 7, 8, 9行はアセンブラ命 令なので実行されない。そのため、メモリーやレジスタの値は空白としている。

この例題で重要なことは、フラグレジスタのSFの値である。ここでの計算は、

$$\begin{aligned}(7FFF)_{16}0(1)_{10} &=(0111111111111111)_2+(000... ...00001)_2 \\ &=(1000000000000000)_2 \\ &=(8000)_{16} \end{aligned}$$

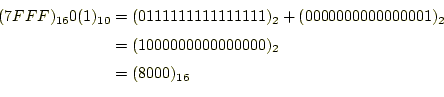を行っている。計算結果が正であっても、第15ビットが1なので、Sign flag(SF)が1と なる。

もし、3行目のADDLの代わりに、ADDAを使うと、GR1の内容は 同じ#8000となるが、フラグレジスターはOV=1, SF=1, ZF=0となる。 オーバーフローフラグが異なる。理由は明らかであろう。

表 2: 教科書List4-6(p.49)の実行例。

行	プログラム			GR1	OF	SF	ZF	AA	BB	CC
1	PGM	START
2		LD	GR1,AA	#7FFF	0	0	0	#7FFF	1	$\ast$
3		ADDL	GR1,BB	#8000	0	1	0	#7FFF	1	$\ast$
4		ST	GR1,CC	#8000	0	1	0	#7FFF	1	#8000
5		RET		#8000	0	1	0	#7FFF	1	#8000
6	AA	DC	#7FFF
7	BB	DC	1
8	CC	DS	1
9		END

2.2 論理減算(SUBL)

2.2.1 内容

命令語	SUBL: SUBtract Logical (subtract:引き算 logical:論理的な)
役割	符号無し整数の引き算を行う命令。
書式	教科書(p.50)の通り。
機能	教科書(p.50)の通り。
フラグレジスタ	教科書(p.49)の通り。

2.2.2 使用例

      SUBL  GR0,GR1      ;GR0←GR0-GR1
      SUBL  GR0,A        ;GR0←GR0-(アドレスAの内容)
      SUBL  GR0,A,GR1    ;GR0←GR0-(アドレス[A+GR1]の内容)
      SUBL  GR0,=5       ;GR0←GR0-5

教科書の例題を実行したときのメモリーとレジスターの内容を表 3に示す。この例題で重要なことは、フラグレジスタのSFの 値である。ここでの計算は、

$$\begin{aligned}(FFFF)_{16}-(1)_{10} &=(1111111111111111)_2-(000... ...00001)_2 \\ &=(1111111111111110)_2 \\ &=(FFFE)_{16} \end{aligned}$$

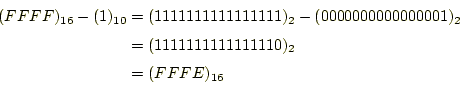を行っている。計算結果が正であっても、第15ビットが1なので、Sign flag(SF)が1と なる。

表 3: 教科書List4-7(p.50)の実行例。メモリーとレジスターの値は、各行の実行の 終了時点での値である。アスタリスク($\ast$)の箇所は未定を表し、実行されない行の 場合は空白としている。

行	プログラム			GR1	OF	SF	ZF	AA	BB	CC
1	PGM	START
2		LD	GR1,AA	#FFFF	0	1	0	#FFFF	1	$\ast$
3		SUBL	GR1,BB	#FFFE	0	1	0	#FFFF	1	$\ast$
4		ST	GR1,CC	#FFFE	0	1	0	#FFFF	1	#FFFE
5		RET		#FFFE	0	1	0	#FFFF	1	#FFFE
6	AA	DC	#FFFF
7	BB	DC	1
8	CC	DS	1
9		END

ホームページ: Yamamoto's laboratory
著者: 山本昌志