5 モンテカルロ積分法
5.1 単純な場合(2次元の面積)
ここでは、モンテカルロ法(Monte Carlo method)呼ばれる乱数を使った一風変わった数値 積分の方法を示す。モンテカルロとは有名なモナコのカジノで、博打をするところである。 この方法を少し学習すると、名前の由来が分かったような気になるはずである。。
まずは、図4の様な円の面積を求めることにする。もちろん、この
円の面積は![]() と分かっているが、これを乱数を用いて数値計算しようと言うのである。
円を囲む正方形内部には、ランダムな点がある。正方形内部にある点の個数を
と分かっているが、これを乱数を用いて数値計算しようと言うのである。
円を囲む正方形内部には、ランダムな点がある。正方形内部にある点の個数を![]() 、円の
内部にある個数を
、円の
内部にある個数を![]() とする。そして、正方形の面積を
とする。そして、正方形の面積を![]() 、円を
、円を![]() とする。する
と、これらには
とする。する
と、これらには
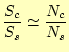 |
(16) |
の関係がある。ランダムな点の数増加させると、これらは、ほとんど等式で結ばれるであ ろう。形状が単純な正方形の面積
と計算できる。点の数を増やすと、それがランダムに分布する限り、右辺は円の面積に近 づく。正方形の面積と点の数を計算するだけで円の面積が分かるのである。このようにラ ンダムな点(乱数)を用いて、積分する方法をモンテカルロ積分と言う。
円の面積を求めても大したことはないが、例えば図5のよ
うな複雑な形状の面積が計算できるとなるとぐっと御利益はある。先ほどの円の面積と同
じようにして、計算できるのである。計算したい部分内の点の数![]() は、
は、
| (18) |
こうやって、内部の点の数を調べて、後は、式(18)のようにすれ ば面積を求めることができる。
このように複雑な領域の積分でも適用でき、応用範囲の広い方法である。積分の
精度を上げようとすると、サンプル数![]() を増やすことになる。しかし、その精度は、た
かだかサンプル数の平方根に比例するのみである。誤差を1/10にしたければ、サンプル数
を100倍にする必要がある。これが、この方法の最大の弱点である。
を増やすことになる。しかし、その精度は、た
かだかサンプル数の平方根に比例するのみである。誤差を1/10にしたければ、サンプル数
を100倍にする必要がある。これが、この方法の最大の弱点である。
精度がサンプル数の平方根に比例するのは、完全な乱数を仮定しているからである。それ を計算機で発生させることは不可能なので、その生成も問題となる。できるだけ良い乱数 を使わなくてはならないが、この問題は奥が深い。ここではこれ以上立ち入らないが、興 味のある者は調べてみると良い。
話は変わるが、ひとつ注意を与えておく。実際のプログラムでは、乱数を使って![]() を発生させて、それが内部にあるか否かをその場で判断する。配列に座標データを入れて、
最後に検査するとメモリーがいくらあっても足りなくなるからである。
を発生させて、それが内部にあるか否かをその場で判断する。配列に座標データを入れて、
最後に検査するとメモリーがいくらあっても足りなくなるからである。
|
|
5.2 複雑な積分
もう少し複雑な積分が必要な場合を考えてみよう。ある関数となる。ここで、
積分を計算するために、まずは体積である。先ほどは、二次元問題であるが、はかなり複
雑な形状の面積をモンテカルロ積分で計算する方法を示した。2次元と同じ考えで、3次元、
4次元、![]() 、M次元の体積も比較的、容易に求めることができる。分かり切った体積
に、領域
、M次元の体積も比較的、容易に求めることができる。分かり切った体積
に、領域![]() を包み込み、その内部にランダムに配置されたサンプル点の数を数えれ
ば良いのである。体積の計算は簡単である。
を包み込み、その内部にランダムに配置されたサンプル点の数を数えれ
ば良いのである。体積の計算は簡単である。
残りは、体積内部の平均
![]() である。これも簡単で、領域
である。これも簡単で、領域![]() 内部
にあるサンプル点の平均より求めることができる。即ち、
内部
にあるサンプル点の平均より求めることができる。即ち、
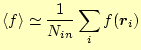 領域 領域 |
(20) |
となる。ここで、
以上より、モンテカルロ法を用いると、体積![]() と平均値
と平均値
![]() の近似値が
計算できることが分かる。従って、式(20)の近似値を求めることが
できる。
の近似値が
計算できることが分かる。従って、式(20)の近似値を求めることが
できる。
数値計算で有名な本「NUMERICAL RECIPES in C」 [1]には、図 6の様な形状の重心を求める問題が出ている。このように複雑な積 分が必要なときにモンテカルロ法は威力を発揮する。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年1月25日
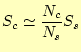
![\includegraphics[keepaspectratio, scale=1.0]{figure/MonteCarlo.eps}](img54.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/MonteCarlo_complex.eps}](img55.png)
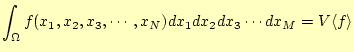
![\includegraphics[keepaspectratio, scale=0.5]{figure/NRC_example.eps}](img66.png)