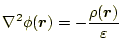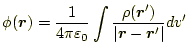1 電荷分布と電場
1.1 電場の求め方
電荷分布が与えられたときに電場を求める方法は、今まで学習した3つの方法- 電場の重ね合わせを使う方法
- ガウスの定理を使う方法
- スカラーポテンシャルを微分する方法
1.1.1 電場の重ね合わせ
最初の方法は、クーロンの法則をそのまま適用して、電場を計算することで ある。これは、最も原始的で最も効率の悪い方法であるので、通常は使われな い。クーロンの法則
と電場の定義式
から、離散的な電荷
である。これを連続的電荷分布
となる。このベクトルの式を、成分で書き表すと、
となる。もちろん、
クーロンの法則を直接使って計算するような問題は、次のようなものがある。
- 問
- 距離
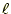 離れて、2つの電荷
離れて、2つの電荷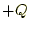 と
と が存在する。その2つの電
荷の直線上での電場を求めよ。
が存在する。その2つの電
荷の直線上での電場を求めよ。
1.1.2 ガウスの法則
先週の授業でやったように、クーロンの法則から、ベクトル解析の知識を使う とガウスの法則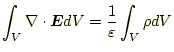 |
積分形 | (6) | |
| 微分形 | (7) |
を導くことができる。実際に、電場を計算する場合、この積分系を使うことが 多い。
例えば、次のような単純な例を解く場合である。この単純な例ですら、クーロ ンの法則を直接適用して、計算できないことが分かる。対称性の良い問題の場 合は、ガウスの法則は強力である。
- 問
- 半径
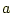 の球の中に、電荷密度
の球の中に、電荷密度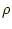 で電荷が一様に分布している。
球の内外での電場を求めよ。
で電荷が一様に分布している。
球の内外での電場を求めよ。
1.1.3 スカラーポテンシャル(電圧)
3つめの方法は、スカラーポテンシャルを求めて、それを微分することにより 電場を計算する方法である。この方法が、最も汎用的で、複雑な問題を解く場 合、一般的に用いられる。先週、示したようにスカラーポテンシャルは、
| (8) |
と定義される。このスカラーポテンシャルが満たす方程式は、この式を微分形 のガウスの法則に放り込めば導くことができる。これは、ポアソン方程式
と呼ばれる、偏微分方程式である。今までの、クーロンの法則やガウスの法則 から電場を計算する場合、ベクトルの演算が必要で大変であった。しかし、こ のポアソン方程式は、スカラーなので、計算量が減り楽である。ただし、電場 を求める場合、このスカラーポテンシャルの微分が必要ではある。
先週述べたように、このポアソン方程式の一般解は、
である。微分方程式(9)、あるいは積分の式 (10)を計算して、スカラーポテンシャル
| (11) |
次のような問題に、このスカラーポテンシャルを適用できる。
- 問
- 半径
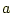 の円板に面密度
の円板に面密度 で電荷が一様に分布していると
き、円板の中心軸にそって、円板の中心から
で電荷が一様に分布していると
き、円板の中心軸にそって、円板の中心から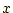 の距離での電場を求
めよ。
の距離での電場を求
めよ。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月28日
![\includegraphics[keepaspectratio, scale=0.7]{figure/E_by_dq.eps}](img5.png)

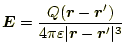
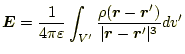
![\begin{equation*}\left\{ \begin{aligned}E_x&= \frac{1}{4\pi\varepsilon}\int_{V^\...
...t]^{3/2}} dx^{\prime}dy^{\prime}dz^{\prime} \end{aligned} \right.\end{equation*}](img12.png)