3 ローレンツ力

エルステットの磁場に関する発見を定量的に述べるためには、磁場と言うもの を定義しなくてはならない。最初の方の授業で述べたように、無限に長い平行 に張られた電線に電流を流すと、それらには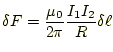

$$\delta F=\frac{\mu_0}{2\pi}\frac{I_1I_2}{R}\delta \ell$$ (10)

のような力が加わる(教科書の式(1.7))。これから、電流を定義する。そして、 電流$I_1$が作る磁場は、そこに流れる電流$I_2$に生じる力

$$F=BI_2$$ (11)

と定義する。すると、磁場は

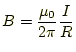$$B=\frac{\mu_0}{2\pi}\frac{I}{R}$$ (12)

となる。これをベクトルで書くと、式 (1)のようになる。これから、あるいは ビオ-サバールの法則から、磁場を定義できる。

これとは別に、磁場を荷電粒子が運動するときの力、

$$\boldsymbol{F}=Q(\boldsymbol{E}+\boldsymbol{v}\times\boldsymbol{B})$$ (13)

から定義できる。この力をローレンツ力と言う。これが、磁場の定義なのか、 実験結果なのか、はたまたなんなのかは意見の分かれるところではあるが、以 下の事実は変わりない。

• クーロンの法則と特殊相対性理論から、この式を導くことは可能であ る。

電場をローレンツ変換すると、磁場の項がでるのである。この辺の詳しい話は、 省略する。

この後のアンペールの力とローレンツ力のパラドックスは、教科書の通り。教 科書に基づいて説明する。

ホームページ: Yamamoto's laboratory
著者: 山本昌志