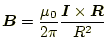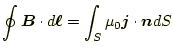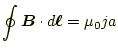2 電流間に働く力と磁場

2.1 磁場

1本の直線電流$I$のつくる磁場 $\boldsymbol{B}$は

$$\boldsymbol{B}=\frac{\mu_0}{2\pi}\frac{\boldsymbol{I}\times\boldsymbol{R}}{R^2}$$ (1)

となる。この式から、半径$r_0$での線積分は

$$\begin{aligned}\oint\boldsymbol{B}\cdot d\ell &=\oint\frac{\mu_... ...rac{\mu_0}{2\pi}\frac{I}{r_0}r_0d\theta &=\mu_0 I \end{aligned}$$

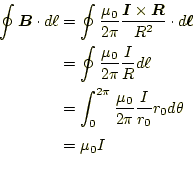となる。この結果は、磁場が直線電流からの距離の$1/R$に比例することから、 容易に予想できる結果である。重要なことは、直線電流からある距離離れた磁 場の線積分は、距離に依存しないことである。

これは、ガウスの法則、点電荷の作る電場の面積分が、距離に依存しないのと 同じである。この場合も、最初、球の中心に点電荷を置き、一般的に閉じた面 で成り立つことを示した。同じことを、ここでも行う。教科書の方法を詳しく 説明する。積分路を変形させると、 $\delta\boldsymbol{\ell}=\delta\boldsymbol{t}+\delta\boldsymbol{r}+\delta\boldsymbol{z}$と書くことがで きる。磁場の方向、すなわち $\boldsymbol{I}\times\boldsymbol{R}$の方向は、$\delta t$に平 行で、$\delta r$と$\delta z$には垂直となる。したがって、積分は先ほどと 同じで、

$$\begin{aligned}\oint\boldsymbol{B}\cdot d\ell &=\oint\frac{\mu_... ...i}\frac{\mu_0}{2\pi}\frac{I}{r}rd\theta &=\mu_0 I \end{aligned}$$

となる。閉じた線路での積分はいつも同じ値になる。今までは、1本の直線電 流であったが、磁場は重ねあわせができるので、複数本でも成り立つ。あるい は、電流がデルタ関数のように離散的ではなく、連続的な分布で、ある密度 ( $\boldsymbol{j}$)として存在する場合も成り立つ。これらは、磁場が重ね合わせの原 理が成り立つからである。したがって、

$$\oint\boldsymbol{B}\cdot d\boldsymbol{\ell}=\int_S\mu_0 \boldsymbol{j}\cdot\boldsymbol{n}dS$$ (4)

となる。右辺は、線積分を囲む電流の総和になっていることに注意が必要であ る。

ところで、この積分の外側の電流の寄与はどうなるのであろうか?。外側の電 流であろうとも、この積分路には磁場を発生させる。結論を先に言うと、

• 外側の電流による磁場はあるが、積分を行うとゼロになる。

である。このことは、電荷でやったのと同じことを行えばよい。

2.2 磁場の回転

式(4)の積分範囲を十分小さくすれば、その微分の法 則が得られる。面積分の面の法線方向は電流の方向として、その範囲を非常に 小さくすると、式(4)は

$$\oint\boldsymbol{B}\cdot d\boldsymbol{\ell}=\mu_0 j a$$ (5)

となる。$a$が積分範囲の面積である。これの極限と取る操作をすると、

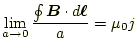$$\lim_{a\to 0}\frac{\oint\boldsymbol{B}\cdot d\boldsymbol{\ell}}{a}=\mu_0 j$$ (6)

となる。この式の左辺は、回転の定義であるので、

$$\nabla\times\boldsymbol{B}=\mu_0 \boldsymbol{j}$$ (7)

と書き改めることができる。スカラーの式がベクトルになったことは、少しカ ンベンしてほしい。ちゃんとすれば、これらの曖昧さもなくなるはず。

あるいは、式(4)をストークスの定理を用いて、

$$\begin{aligned}\int_S\mu_0 \boldsymbol{j}\cdot\boldsymbol{n}dS ... ...t_S\nabla\times\boldsymbol{B}\cdot \boldsymbol{n}dS \end{aligned}$$

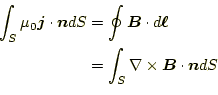と変形する。これから、式(7)を導くことができる。

これで、磁場の回転が求まったわけである。安心するのはまだ早い。磁場を決 めの式は、もうひとつ必要である³。磁場の発散を求めなくてはならない。

2.3 磁場の発散

今まで、考えてきた、1本の長い電線が作る磁場を考えよう。磁場は、電線の 周りに回転としてできる。このような場合、どのような微小の体積を考えても、 その発散はゼロである。要するに、どんな部分をとっても、入ってくる磁場の フラックスと出て行くフラックスは等しい。これは、たとえ、電線を取り囲ん だ体積を考えても、そうなる。

電場の場合は、電荷から電気力線が出ていて、どこか無限遠点に行くか、反対 の電荷に吸収されていた。磁場の場合、磁力線は閉じた線である。このことが 正しいとすると、磁場の発散

$$\nabla\cdot\boldsymbol{B}=0$$ (9)

となる。いままで、この式に反する観測結果は得られていない。したがって、 この磁場に関する発散の式は正しいとする。この式は、電荷に相当する磁荷は 無いと言っている。

これで、磁場に関する回転と発散の式が得られたので、磁場を計算することが できるようになった。とりあえず、めでたい。

ホームページ: Yamamoto's laboratory
著者: 山本昌志