1 真空中の静電場
問題3.1
| [問] | 真空中で半径 |
|---|
球の中心を座標の原点においても問題の意味は変わらないので、そうする。対 象性から、
- 電場
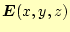 の向く方向は、原点と
の向く方向は、原点と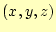 を結ぶ直線上であ
る。
を結ぶ直線上であ
る。
- その大きさは、位置ベクトルの大きさ
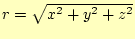 の関数の
はずである。
の関数の
はずである。
![]() は
は![]() のみの関数なので、原点からの距離が同じ場所では、同じ値を持つ。
このように対象性が良く、電場の値が同じ場合、ガウスの法則から電場を求め
るのが都合が良い。図1のように半径
のみの関数なので、原点からの距離が同じ場所では、同じ値を持つ。
このように対象性が良く、電場の値が同じ場合、ガウスの法則から電場を求め
るのが都合が良い。図1のように半径![]() の球でガウス
の法則を適用する。ガウスの法則の微分形は
の球でガウス
の法則を適用する。ガウスの法則の微分形は
| (1) |
である。両辺を半径
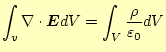 |
(2) |
となる。左辺はガウスの定理により変形し、右辺は電荷分布が一様と言う条件 を使うと
となる。ここで、電場ベクトル
| (4) |
となる。この結果を、式(3)に代入すると
 |
(5) |
となる。また、対象性により、
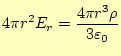 |
(6) |
となる。したがって、電場は、
| (7) |
となり、原点からの距離
問題3.2
| [問] | 原子の内部には球対象な電荷分布があると考えられる。その
電荷分布による電位は、たとえば、
|
|---|
このようなポテンシャルをYukawa型と言う。電位![]() が分かっていて、電荷
分布
が分かっていて、電荷
分布![]() を求める問題は簡単で、それらの関係を示すポアソン方程式
を求める問題は簡単で、それらの関係を示すポアソン方程式
を使えばよい。ここで、問題は球対称なので、極座標のラプラス演算子を使う のが適当である。もちろん、デカルト座標で計算しても良いが、それは大変で ある。付録に極座標の勾配と発散、回転、ラプラス演算子を示す。そのラプラ ス演算子をつかうと
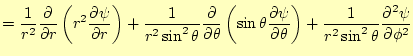 |
||
| 問題の電位 |
||
![$\displaystyle =\frac{1}{r^2}\frac{\partial}{\partial r} \left[r^2\frac{\partial}{\partial r}\left(\frac{e^{-\alpha r}}{r}\right) \right]$](img27.png) |
||
 |
(9) |
となる(教科書の解答は間違っている)。これらから、ポアソン方程式 (8)より、電荷分布は
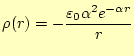 |
(10) |
となる。
問題3.3
| [問] | 2個の点電荷 |
|---|
点電荷![]() がつくる電位は、そこから無限遠点をゼロとの電位として、
がつくる電位は、そこから無限遠点をゼロとの電位として、
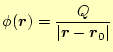 |
(11) |
と表すことができる。
より一般的な座標系で問題を解くので、問題の![]() の電荷量を
の電荷量を![]() 、位置を
、位置を
![]() とする。同様に、
とする。同様に、![]() の電荷量を
の電荷量を![]() 、位置を
、位置を
![]() とする。すると、2つの電荷が作る電位は、
とする。すると、2つの電荷が作る電位は、
となる。問題は、
 |
(13) |
となり、ちょっとだけ計算を進めると、
| (14) |
が得られる。この絶対値がじゃまくさいので、最後の式の両辺を2乗する。そうす ると
| (15) |
となる。ベクトルの2乗は、内積になることに気をつけて計算を進める。
| (16) |
| (17) |
これを、もう少し簡単にするために
 |
(18) |
と変形する。そして、ベクトルの式に書き直す。
![$\displaystyle \left[\boldsymbol{r}+\left(\frac{Q_1^2}{Q_1^2-Q_2^2}\boldsymbol{r}_2 -\frac{Q_2^2}{Q_1^2-Q_2^2}\boldsymbol{r}_1\right)\right]^2=$](img49.png) |
(19) | |
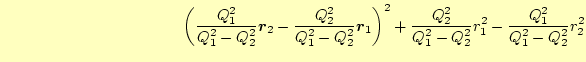 |
(20) |
もう少し、式を整理する。
![$\displaystyle \left[\boldsymbol{r}-\left(\frac{Q_2^2}{Q_1^2-Q_2^2}\boldsymbol{r...
...= \left[\frac{Q_1Q_2(\boldsymbol{r}_1-\boldsymbol{r}_2)} {Q_1^2-Q_2^2}\right]^2$](img51.png) |
(21) |
そして、最後にベクトルの大きさの式に直すと、
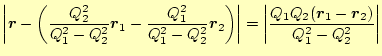 |
(22) |
となる。これは、中心が
電位がゼロ以外の等電位面は球になるだろうか?。アポロニウスの円との関わ りは、各自調べよ。本当はアポロニウスの円を説明してから、この問題を解く のが定石。
問題3.4
| [問] | 無限に広い平面上に、一様な面密度 |
|---|
この問題は、電荷が無限に広い平面上に広がっているため、有限領域に電荷が あるときのポアソン方程式の解
 |
(23) |
を使うことはできない。このような場合は、ガウスの法則の式 (3)を使うのが良い。問題の対称性から、
- 電場の方向はその面の法線方向か、その反対である。即ち、図 2のzか-z方向である。
- 電荷が分布している平面の両側で電場の向きは反対で、その大きさは 同じである。
- 電場の大きさは、xおよびy方向に移動しても変わらない。
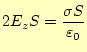 |
(24) |
となる。したがって、問の電場は、
となる。電場の大きさはどこでも一定である。
通常であれば、無限遠![]() の電位をゼロとして、積分を行い電位を求め
る。しかし、この場合はそんなに単純ではない。無限の広さに電荷が分布して
いるため、無限遠をゼロの電位にすると、積分の値が発散する。これは問題が
あるので、基準電位を変えなくてはならない。
の電位をゼロとして、積分を行い電位を求め
る。しかし、この場合はそんなに単純ではない。無限の広さに電荷が分布して
いるため、無限遠をゼロの電位にすると、積分の値が発散する。これは問題が
あるので、基準電位を変えなくてはならない。
そこで、電位の定義の式
| (26) |
を考える。電位を微分すると、電場になるので、式 (25)になるものを探す。それは、
| (27) |
である。積分定数
問題3.5
| [問] | 半径 |
|---|
この問題は、ポテンシャル(電位)を求めてから、電場を計算するのが簡単であ る。ポテンシャルは
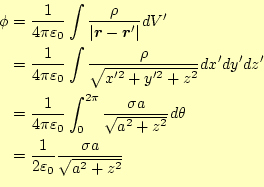 |
となる。ポテンシャルが分かったので、電場は直ちに
![\begin{equation*}\begin{aligned}\boldsymbol{E}&=-\nabla\phi &=\left[0, 0, \f...
...\sigma a}{2\varepsilon_0}\frac{z}{(a^2+z^2)}\right] \end{aligned}\end{equation*}](img65.png) |
とわかる。
問題3.6
| [問] | 点電荷 |
|---|
まずは、極座標系で計算を行う。極座標系で書いた電位は
となり、
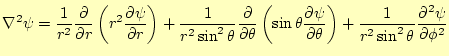 |
(31) |
である。この式に、点電荷の電位を表す式 (30)を代入して計算すればよい。電位は、
 |
となる。
問題3.7
| [問] | 半径 |
|---|
同心円筒コンデンサーは、図4のような形状をし ている。コンデンサーで重要なことは、
- コンデンサーの2つの電極には、片方に
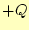 の電荷が蓄えられると、もう
片方は正確に
の電荷が蓄えられると、もう
片方は正確に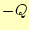 となる。合計すると、必ずゼロになる。
となる。合計すると、必ずゼロになる。
- 合計すると電荷はゼロとなるので、外部には電場は無い2。
それでは、問題を解くことにするが、まずは対称性を考える。問題の対象性よ り、
- 電場の方向は、電極の法線方向か、その反対である。
- コンデンサーの全長は、その半径に比べて、十分長いと仮定する。す ると、図の上下方向での電場の変化は無視できる。
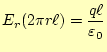 |
(33) |
となる。したがって、コンデンサー内部の電場は
| (34) |
である。
 |
となる。単位長さあたりの容量
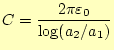 |
(36) |
である。トータルの容量は、これにコンデンサーの全長
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年12月28日

![\includegraphics[keepaspectratio, scale=0.9]{figure/sphare_charge.eps}](img19.png)

![\includegraphics[keepaspectratio, scale=0.7]{figure/infinite_plane_charge.eps}](img63.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/ring_charge.eps}](img66.png)
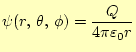
![\includegraphics[keepaspectratio, scale=0.7]{figure/coaxial_capaciter.eps}](img82.png)