1 真空中の静磁場
問題4.1
| [問] | 1本の直線電流のまわりの磁場を、例題ではベクトルポテン シャルを直接計算することによって求めた。別解として、一本の直線上に一 様な線密度で電荷が分布しているときの、電位の計算と対比させることによっ ても、いまの磁場が求められることをしめせ。 |
|---|
電場のスカラーポテンシャルが満たす微分方程式は、
| (1) |
である。一方、磁場のベクトルポテンシャルの場合は
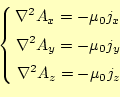 |
である。スカラーポテンシャルもベクトルポテンシャルも同じ微分方程式であ る。微分方程式が同じならば、その解も同じ形である。
まずは、単純なスカラーポテンシャルを計算する。線密度![]() で電荷が一
様に分布している無限に長い線を考える。ガウスの法則を使うと、電場は
で電荷が一
様に分布している無限に長い線を考える。ガウスの法則を使うと、電場は
| (3) |
となる。次にポテンシャルを計算する。この場合、無限の電荷があるので、無 限遠点を基準電位にできない。
 |
である。微分方程式が同じなので、この結果は直ちにベクトルポテンシャルに 応用できる。その結果、
 |
(5) |
となる。これが、無限に長い直線電流の磁場を表すことは、各自確かめよ。
問題4.2
| [問] | 次のベクトルポテンシャルは、同一の磁場を表している。そ の磁場の磁束密度を求めよ。次に、一つの磁場を表すのに、このような複数 のベクトルポテンシャルがあってもよい理由を述べよ。 |
|---|
まず、それぞれのベクトルポテンシャルが表す磁場を考えてみる。ベクトルポ テンシャルと磁場の関係は、
となる。同様に、式(7)の表す磁場は、
となる。これら2つのベクトルポテンシャルは、同じ磁場
なぜ、ベクトルポテンシャルは異なっているのに、同じ磁場となるのか?。こ れは、ベクトル恒等式
| (10) |
から説明できる。即ち、異なるベクトルポテンシャル、
それでは、
![]() 、
、
![]() として、そ
の関係を調べてみる。それぞれの差は、
として、そ
の関係を調べてみる。それぞれの差は、
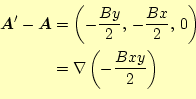 |
である。したがって、
問題に対する解答は、これで終わりであるが、もう少し違った見方で、この問 題を見てみる。式(6)のベクトルポテンシャルと磁場の 様子を図1に示す。この図の矢印がベクトルポテンシャ ルで、磁場は紙面に垂直にある。式(7)の図 3のようになる。これは、式 (8)や(8)の通りである。図を 見れば、矢印が川の流れを表すとすると、紙面に垂直な軸をもつ水車を入れる とそれが回ることが分かるであろう。その回転速度もどこでも同じであること が直感で理解できると思う。
次に、図1を90度回転させてみよう。すると、図 2のようになるであろう。90度回転させても磁場はまっ たく変化しないが、ベクトルポテンシャルの方向は変化する。この90度回転し たベクトルポテンシャル
もまた、同じ磁場を表すことが予想できる。実際、これが現す磁場を回転を取 ると、
図3のベクトルポテンシャルは、図
1と2を加算して、2で割っ
た形になっている。それぞれのベクトルポテンシャルを、
![]() とすると、
とすると、
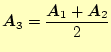 |
(13) |
である。これから、図3の磁場
 |
となることが理解できるであろう。問題で与えられたベクトルポテンシャル図 3は、図1と90度回転した図 2を足して2で割っただけである。図1と 2が0.5ずつ寄与しているのである。
このことから、図1の寄与が![]() で図
2が
で図
2が![]() のような、図の場合でも同じ磁場を表す。ま
た、それを45度回転させても同じ磁場を表す。
のような、図の場合でも同じ磁場を表す。ま
た、それを45度回転させても同じ磁場を表す。
問題4.3
| [問] | 半径 |
|---|
問題のコイルの1個が軸上に作る磁場![]() は、対称性により、軸上磁場は軸の方
向に向いているはずである。その様子を図6
の左の絵で示す。このコイルの小さい電流要素
は、対称性により、軸上磁場は軸の方
向に向いているはずである。その様子を図6
の左の絵で示す。このコイルの小さい電流要素![]() が作る磁場は、ビオ-
サバールの法則
が作る磁場は、ビオ-
サバールの法則
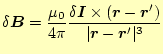 |
(15) |
から計算できる。これから、その磁場は図6 の右の絵のようになる。軸上の磁場
図から分かるように、微小磁場
![]() は軸の垂直成分もある。しかし、
これは、コイル1週にわたって足し合わせると、ゼロになる。コイル1周にわたっ
て合計すると、残るのは軸上の成分のみである。コイルの軸上の成分は、
は軸の垂直成分もある。しかし、
これは、コイル1週にわたって足し合わせると、ゼロになる。コイル1周にわたっ
て合計すると、残るのは軸上の成分のみである。コイルの軸上の成分は、
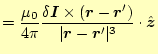 |
||
|
|
||
|
|
||
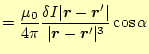 |
||
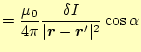 |
||
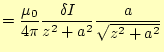 |
||
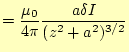 |
(16) |
となる。これをコイルの全ての電流で積分することになるが、
となる。これで準備ができた。あとは、ヘルムホルツコイルになるように、座 標を設定するだけである。
ヘルムホルツコイルは、図7のような構成になって
いる。この2つのコイルの中心を![]() とする。この場合、左右のそれぞれのコ
イルが作る磁場は、式(17)を用いると、
とする。この場合、左右のそれぞれのコ
イルが作る磁場は、式(17)を用いると、
![$\displaystyle =\frac{\mu_0}{2}\frac{a^2I}{[(z+\frac{a}{2})^2+a^2]^{3/2}}$](img64.png) |
左のコイル | (18) | |
![$\displaystyle =\frac{\mu_0}{2}\frac{a^2I}{[(z-\frac{a}{2})^2+a^2]^{3/2}}$](img66.png) |
右のコイル | (19) |
と計算できる。
次に![]() 付近の磁場の一様性を調べる。そのために、それぞれのコイルが作
る磁場について、
付近の磁場の一様性を調べる。そのために、それぞれのコイルが作
る磁場について、![]() の周りでテイラー展開する。展開の結果は
の周りでテイラー展開する。展開の結果は
![$\displaystyle =\frac{\mu_0a^2I}{2}\left[ \frac{8}{5\sqrt{5}a^3} -\frac{48}{25\s...
...frac{1152}{625\sqrt{5}a^7}z^4 -\frac{5376}{15625\sqrt{5}a^8}z^5 +O(z^6) \right]$](img68.png) |
(20) | |
![$\displaystyle =\frac{\mu_0a^2I}{2}\left[ \frac{8}{5\sqrt{5}a^3} +\frac{48}{25\s...
...frac{1152}{625\sqrt{5}a^7}z^4 +\frac{5376}{15625\sqrt{5}a^8}z^5 +O(z^6) \right]$](img70.png) |
(21) |
となる。これから、これら2つのコイルの和であるヘルムホルツコイルの磁場 は
![$\displaystyle =\frac{\mu_0a^2I}{2}\left[ \frac{16}{5\sqrt{5}a^3} -\frac{2304}{625\sqrt{5}a^7}z^4 +O(z^6) \right]$](img72.png) |
(22) |
となる。要するに、ヘルムホルツコイルの中心付近では、
- それぞれのコイルの1次の成分はない。
- 2次と3次の成分は、それぞれのコイルでキャンセルされる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年12月28日

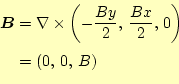
![\includegraphics[keepaspectratio, scale=0.6]{figure/vector_pot_1.eps}](img37.png)
![\includegraphics[keepaspectratio, scale=0.6]{figure/vector_pot_2.eps}](img39.png)
![\includegraphics[keepaspectratio, scale=0.6]{figure/vector_pot_3.eps}](img41.png)
![\includegraphics[keepaspectratio, scale=0.6]{figure/vector_pot_4.eps}](img42.png)
![\includegraphics[keepaspectratio, scale=0.6]{figure/vector_pot_5.eps}](img43.png)
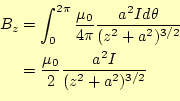
![\includegraphics[keepaspectratio, scale=1.0]{figure/OneTurn_coil.eps}](img61.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/HelmHoltz_coil.eps}](img73.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/Field_HelmHoltz_coil.eps}](img74.png)