1 物質中の電場

原子に電場を加えると、分極が発生し、図1のように電気双極子 $\boldsymbol{p}$として取り扱うことができる。物質中では、これが密度$N$で存在するとして、 それを考慮して分極ベクトル

$$\begin{aligned}\boldsymbol{P}&=Nq\boldsymbol{\delta} &=N\boldsymbol{p} \end{aligned}$$

が定義できる。図からわかるように、ある表面積$S$を通り抜ける総電荷量$Q$ は、

$$\begin{aligned}Q&=-SNq\delta\cos\theta &=-S\boldsymbol{P}\cdot\boldsymbol{n} \end{aligned}$$

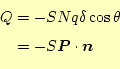である。ここで、 $\boldsymbol{n}$は表面の法線方向である。負号になる理由は、法線 方向と分極ベクトルの定義を考えれば分かるはずである。これから、単位表面あたり 通り抜ける電荷量は、

$$\sigma_p=-\boldsymbol{P}\cdot\boldsymbol{n}$$ (3)

となる。この分極により、閉じた空間の電荷量は

$$\int \rho dV =\int \sigma dS$$

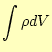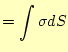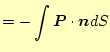$$=-\int \boldsymbol{P}\cdot\boldsymbol{n} dS$$    ガウスの定理より

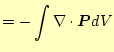$$=-\int \div{\boldsymbol{P}}dV$$ (4)

となる。この積分は任意の領域で成り立つため、

$$\rho_p=-\div{\boldsymbol{P}}$$ (5)

を導くことができる。

次に、この分極ベクトルが作る電流であるが、これは式(3)から、直ちに 導くことができる。

$$\begin{aligned}\boldsymbol{j}_p &=\frac{\partial \boldsymbol{P}}{\partial t} \end{aligned}$$

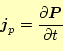これを分極電流と言う。これで、分極ベクトルによる電荷と電流を導くことｇあできたので、誘電体中のMaxwellの方程式を書き直す準備ができた。

図 1: 原子が分極する様子

図 2: 境界を越えての電荷の移動(境界と分極ベクトルが平行)

図 3: 境界を越えての電荷の移動(境界と分極ベクトルが角度を持つ)

ホームページ: Yamamoto's laboratory
著者: 山本昌志