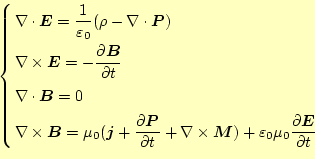3 物質中のMaxwellの方程式について

ミクロ的な立場で見ると、Maxwellの方程式は、

$$\left\{ \begin{aligned}&\div{\boldsymbol{E}}=\frac{\rho}{\varep... ...\frac{\partial \boldsymbol{E}}{\partial t}) \end{aligned} \right.$$

である。電磁場については、これが全てで、これを解けば全て分かる。分極に よる電場も、分極電荷から生じると考えれば、この式で十分である。分極電流 もこれに含むことができる。磁化分極の電流も含めることができる。

しかし、分極電荷が問題となるような微少領域まで考えて、電磁場を計算する のは、いかにも大変である。そこで、マクロ的な立場から、Maxwellの方程式 を書き直す。追加するのは、

$$\left\{ \begin{aligned}&\rho_p=-\div{\boldsymbol{P}} &\boldsy... ...boldsymbol{j}_m=\nabla\times \boldsymbol{M} \end{aligned} \right.$$

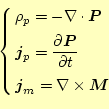である。これに加えて、実電荷(真電荷)による電流と電荷密度がある。これは 一般には、$\rho$と $\boldsymbol{j}$と書かれる。ミクロ的な立場のMaxwellの方程式 (9)の$\rho$と $\boldsymbol{j}$には、電気分極や磁気分極の電 荷密度や電流が含まれるが、以降のマクロ的な立場では、それらは実電荷のみ が担う。

マクロ的な立場で、電気分極や磁気分極による電荷や電流を区別して書いた Maxwellの方程式は、

$$\left\{ \begin{aligned}&\div{\boldsymbol{E}}=\frac{1}{\varepsil... ...0\frac{\partial \boldsymbol{E}}{\partial t} \end{aligned} \right.$$

となる。これは、式(9)の電荷密度や電流の項を、電 気分極、磁気分極、実電荷によるものに分けたのである。これが、物質中での マクロなMaxwellの方程式である。しかし、この式は複雑であまり見通しがよ くない。そこで、ミクロな式(9)に似た式に変形す ることを考える。式(11)を変形すると

$$\left\{ \begin{aligned}&\div{(\varepsilon_0\boldsymbol{E}+\bold... ...\boldsymbol{E}+\boldsymbol{P})}{\partial t} \end{aligned} \right.$$

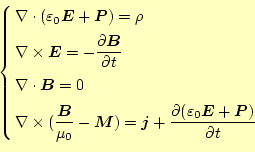が得られる。ここで、新たに

$$\left\{ \begin{aligned}&\boldsymbol{D}=\varepsilon_0\boldsymbol... ...\frac{\boldsymbol{B}}{\mu_0}-\boldsymbol{M} \end{aligned} \right.$$

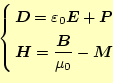を定義する。この $\boldsymbol{D}$を電束密度[C/m$^2$]、 $\boldsymbol{H}$を磁界の強さ[A/m]と言う。 これらを使うと、物質中のMaxwellの方程式は、

$$\left\{ \begin{aligned}&\div{\boldsymbol{D}}=\rho &\nabla\tim... ...+\frac{\partial \boldsymbol{D}}{\partial t} \end{aligned} \right.$$

となる。このままでは、4つのベクトルが未知数であるため、通常は解けない。 物質中では、

$$\left\{ \begin{aligned}\boldsymbol{D}=\varepsilon\boldsymbol{E} \boldsymbol{B}=\mu\boldsymbol{H} \end{aligned} \right.$$

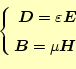という関係がある。この比例定数 $\varepsilon$を物質中の誘電率、$\mu$を物 質中の透磁率という。これは、 $\boldsymbol{P}$は $\boldsymbol{E}$に比例する、 $\boldsymbol{M}$は $\boldsymbol{B}$に比例することから、導くことができる。電場や磁場が弱いときには、 比例するが、大きくなると比例しなくなる。そのため、 $\varepsilon$や$\mu$ を定数として扱うのは近似に過ぎない。

そこで、式(14)がいつでも成り立つためには、 $\varepsilon$や$\mu$を定数として取り扱わないようにすればよい。磁場や電 場の強さの関数であるし、もはや実数として取り扱わない、スカラーではなく 行列(テンソル)、あるいはヒステリシスも考慮に入れ、取り扱う範囲を広げる ことができる。そのようにして、 $\varepsilon$や$\mu$は物質中の電磁気的な 作用を記述している。

最後に、導体中の電磁場を計算する場合は、オームの法則を

$$\boldsymbol{j}=\sigma\boldsymbol{E}$$ (16)

を加えればよい。ここの$\sigma$は、物質中の導電率である。

駆け足でしたが、物質中のMaxwellの方程式は終わり。

ホームページ: Yamamoto's laboratory
著者: 山本昌志