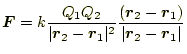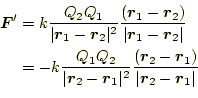3 電荷と電場
電気で最初に勉強するのは、なんといってもクーロンの法則(Coulomb law)で ある。クーロンの法則については、教科書の3章真空中の静電場のところで詳 しく述べるので、法則そのものについては、さらっと聞いて欲しい。その代わ り、基本的な物理の考え方- ベクトルとスカラー
- 作用反作用の法則
- 単位
- 場
- 重ね合わせの原理
3.1 クーロンの法則
教科書では、クーロンの法則はと書いている。これは、図1のように表すことができる。 この式が言っていることは、電荷の積が負の場合引力、正の場合斥力となる。 力の大きさは距離の2乗に反比例し、電荷の積に比例する。
クーロンの法則について、次のことについて考察してみよう。
- 世の中に電荷が2つしかないとする。この場合、それぞれの電荷の大き さ調べる手立てはあるか?。
- それでは、電荷が3つある場合はどうか?
- 電子の電荷は
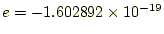 [C]である。電子の電荷が
なぜ負になっているか、考えてみよう?
[C]である。電子の電荷が
なぜ負になっているか、考えてみよう?
- クーロン力は、距離の-2乗に比例する。なぜ、-2という丁度の数字な のか?。これは必然か?。-2.0001では不都合なのか?
- クーロン力は、各々の電荷の積の1乗に比例する。なぜ、1という丁度 の数字なのか?。これは必然か?。1.00001では不都合なのか?
- クーロン力の方向は、2つの電荷の延長線上である。延長線上である必 然はあるか?。他の方向を向くとどのような不都合があるか?
3.2 ベクトルとスカラー
数式を記述する場合、右辺がスカラー量であれば左辺はスカラー量でなくては ならない。右辺がベクトル量であれば、左辺はベクトル量でなくてはならない。 電磁気学を学ぶときには、どれがスカラーでどれがベクトルか良く考えるのが コツである。それでは、式(1)について、以下を確認せよ。
- そもそもベクトル(vector)とは?。スカラー(scalar)とは?。分かりや すい例を挙げよ
- ベクトルは方向と大きさを持つと言われる。方向と大きさはどのよう に表現できるか?
- 式(1)で使われている変数をベクトルとスカラー に分けよ。
- 左辺にある
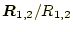 は、何を表しているか?
は、何を表しているか?
 と
と
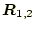 と
と の関係は、どうなっているか?
の関係は、どうなっているか?
- なぜ位置を表すのに、位置ベクトル(position vector)というベクトル 量が使われるのか?。そもそも、位置はベクトルなのか?
3.3 作用・反作用の法則
ベクトル| (2) |
となる。これを利用して、クーロンの法則を書き換えると、
となる。この
である。
| (5) |
の関係があることが分かる。この式は、2つの電荷に働く力の大きさが等しく、 向きが反対であると言っている。これは、作用・反作用の法則と呼ばれるもの である。
3.4 単位について
数学では単位を気にすることは無いが、自然科学では単位は非常に重要である。 自然科学において、等号や不等号で表せる関係式の両辺の単位は、全く同じで ある。単位の異なるもの、たとえば面積と質量は比較できないからである。そ れと同じように、加算や減算を行う場合、その2つの演算対象も同じ単位でな くてはならない。一方、積や除算の場合は、演算対象の単位は異なっても良い。 導いた式が正しいか否か調べる場合、まずは単位を確認することから始めよ。教科書に書かれているように、比例係数
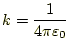 |
(6) |
と、普通は書かれる。真空の誘電率の値とその単位は
![$\displaystyle \varepsilon_0=\frac{10^7}{4\pi c^2}=8.854\times 10^{-12} \qquad \left[\frac{C^2}{N\cdot m^2}\right]$](img19.png) |
(7) |
である。
- クーロンの法則から、この真空の誘電率の単位を導け
3.5 電場
3.5.1 遠隔作用
遠隔作用については、教科書に書いてあるとおりである。図 1の電荷1が電荷2に及ぼす力が、媒介が無くても伝わる と考えるのが遠隔作用である。この解釈は受け入れがたく、通常は使われない。 ニュートンが万有引力の法則を発表したとき、それは遠隔作用で、なかなか受 け入れがたかったようである。何もない真空を通過して、力が伝わることに人々 は難色を示したのである。日常、見たり感じたりする力は、何かの媒質が 介在するものである。液体や固体、気体を通して力は感じるものである。でも、 当時は磁石による力は分かっていて、それは遠隔作用に思える。人々はどのよ うに考えていたのか興味がある2。気とか超能力とか言う人は、遠隔作用を支持しているように思えるが、いかが なものか。
3.5.2 近接作用
近接作用と電場の考え方は、教科書に書いてあるとおりである。これが、現代 的な考え方である。
図1の電荷![]() が直接
が直接![]() に作用するのではない。ま
ず
に作用するのではない。ま
ず![]() は、その近くの空間の物理的な状態を変化させ、それ変化が次々と伝
わり、
は、その近くの空間の物理的な状態を変化させ、それ変化が次々と伝
わり、![]() に達した時点で、それに影響を及ぼす。
に達した時点で、それに影響を及ぼす。![]() は空間(場)に作用を及ぼ
し、
は空間(場)に作用を及ぼ
し、![]() は空間から作用を及ぼされるのである。これは、明らかに遠隔作用
ではなく、近接作用と呼ばれる。これが場の考え方である。
は空間から作用を及ぼされるのである。これは、明らかに遠隔作用
ではなく、近接作用と呼ばれる。これが場の考え方である。
観測される結果が遠隔作用と同じであれば、ただの言い換えに過ぎない。遠隔 作用と近接作用の決定的に異なることがある。それは、作用が伝わる時間であ る。遠隔作用では瞬時に影響が伝わるが、近接作用では有限の時間が必要であ る。観測の結果、影響が伝わる速度は、光速度と同じである。
それでは、クーロン力を伝える電場というものを考える。ある場所に電荷
![]() を置く。すると、その電荷は
を置く。すると、その電荷は
![]() の力を受けたとする。場の考
え方では、そこの電場
の力を受けたとする。場の考
え方では、そこの電場
![]() が作用して、力が生じたとする。すなわち、
が作用して、力が生じたとする。すなわち、
| (8) |
である。これが電場の定義と考えても良い。
- 電場の定義とクーロンの法則を用いて、電荷
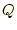 が作る電場を表す式を
求めよ。
が作る電場を表す式を
求めよ。
3.6 重ね合わせの原理
クーロンの法則、式(1)から、電荷の作用は加算できるこ とが分かる。これは、2つの電荷に作用するクーロン力は、他の電荷に影響さ れないことを意味する。重ね合わせの原理の例として、3つの電荷がある場合 を考える。1番目の電荷に働く力は、2番目からの影響と3番目からの影響を足 し合わせたものになる。すなわち、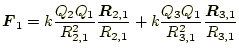 |
(9) |
となる。これは、3個の場合であるが、いくら電荷があってもこれは成り立つ。
- この力の重ねあわせが成り立てば、電場の重ね合わせの原理が成り立 つことを示せ。
3.7 位置エネルギー
この辺については、教科書の補足にとどめる。万有引力の法則は、
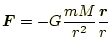 |
(10) |
である。ここで、
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月27日
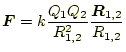
![\includegraphics[keepaspectratio, scale=0.7]{figure/Coulomb_low.eps}](img5.png)