2 電流と磁場
2.1 電流とは何か
電磁気学で表れる電流は、2種類ある。荷電粒子の移動から生じるものと、電 場の変化から生じる。前者を伝導電流、後者を変位電流と言う。ここでは、伝 導電流のみを取り扱うことにする。電線に電池を接続すると、伝導電流が流れる。電池をつなぐことで、電線内に 電場が生じ、自由電子が電場による力を受け移動するのである。この電子の移 動が電流となる。金属中では電子であるが、水溶液中ではイオンの場合もある。 荷電粒子であれば、種類は関係なく、それが移動すれば電流となる。
電流![]() の大きさは、そこを通過する単位時間当たりの電荷量
の大きさは、そこを通過する単位時間当たりの電荷量![]() である。式で表現する
と、
である。式で表現する
と、
となる。これで、電荷と電流の関係を示すものである。
- 金属中の電子の移動の速度は非常に遅い。大体の速度を求めよ。
2.2 アンペールの力
平行な2本の電線に同じ方向に電流を流すと、各々の電線が引き付けあう力、 引力が働く(図1)。反対方向に電流を流すと、斥力が働く。 実験の結果、その力は、ということが分かった。ここで、
この力は、モーターを動かす力となって利用されている。電流を制御すること により、磁場の強さ制御し、モーターの力をコントロールするのである。
真空の透磁率![]() は、
は、
| (3) |
と定義されている。力は別の方法で定義されている(
電流が定義できたので、式(1)を用いて、電荷の定義ができる。
| 物理量 | 単位の名称 | 単位記号 | 定義 |
| 長さ | メートル | m | 光が(1/299792458)秒間に真空中を伝わる距離。 |
| 質量 | キログラム | kg | 国際キログラム原器の質量。これは1 気圧、最大密度の温度にある水1リットルの質量にほぼ等しい。 |
| 時間 | 秒 | s | |
| 電流 | アンペア | A | 真空中1[m]間隔で平行に置かれた無限に小さい円断面積を有する無限に長
い2本の直線導体上のそれぞれを流れ、これらの導体の1[m]ごとに
|
| 熱力学温度 | ケルビン | K | 水の三重点の熱力学温度の1/273.16 |
| 物質量 | モル | mol | 0.012[kg]の |
| 光度 | カンデラ | cd | 周波数が
|
2.3 磁場
電荷が作る場は、その部分に働く力から定義できた。単位電荷の受ける力の方 向と大きさが電場である。同じような考え方で、電流が作る場、磁場というも のを考えることができる。単純な例として無限に長い電線が作る磁場を考えよ う。図1のように、平行に置かれた2本の電線を考える。一方 の電線には、電流となる。これから、磁場
本当は、力![]() と磁場
と磁場![]() 、電流
、電流![]() はベクトルであるが、ここではスカラーで
書いている。左辺はベクトル、右辺にベクトルが掛け算で出てきているので、
ベクトル積が関係することは想像できる。これについては、後の授業で詳細に
行うので、ここでは気にしないで欲しい。
はベクトルであるが、ここではスカラーで
書いている。左辺はベクトル、右辺にベクトルが掛け算で出てきているので、
ベクトル積が関係することは想像できる。これについては、後の授業で詳細に
行うので、ここでは気にしないで欲しい。
磁場![]() のことを、磁束密度という。式(4)から、磁束密度の
単位は[
のことを、磁束密度という。式(4)から、磁束密度の
単位は[
![]() ]となる。MKSA単位系で書くと、
[
]となる。MKSA単位系で書くと、
[
![]() ]となる。通常はこれらに代わって、
[
]となる。通常はこれらに代わって、
[![]() ]や[T]という単位が使われる。
]や[T]という単位が使われる。![]() はウェーバと
はウェーバと![]() はテスラと読む。
はテスラと読む。
- 磁場の単位が、mksA単位で[
 ]となること
を示せ。
]となること
を示せ。
この磁場の定義式(4)と式(2)から、長 い電線が作る磁場は、
 |
(5) |
となる。磁場の方向は、図2の磁束線の接線方向である。な ぜ、そのような方向を向くかは、後の講義で示す。
2.4 磁場を図に表す方法
この磁場を表す方法は、電場を表す方法と同様の方法がある。それぞれの方法 を、図3と4に示す。これは、直 径6[cm]の無限に長い銅線に電流を1[A]流し、一辺200[cm]の鉄でその銅線を囲っ たときの磁場の様子である。図3は、その点での磁場のベクトルが矢印で示している。 4の方は、磁束線を表し、磁束線の接線が磁場のベク トルの方向である。そして、磁束線の密度が磁場の強さを表す。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月27日
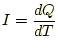

![\includegraphics[keepaspectratio,scale=0.7]{figure/Amper_force.eps}](img11.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/define_B.eps}](img30.png)
![\includegraphics[keepaspectratio,scale=0.3]{figure/wire_arrow.eps}](img31.png)
![\includegraphics[keepaspectratio,scale=0.3]{figure/wire_conture.eps}](img32.png)