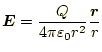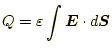2 先週の復習(ベクトル場の発散)

2.1 ベクトル場の発散とクーロンの法則

2.1.1 大きな領域での話

先週は教科書の沿って、ガウスの法則を説明した。その骨子は、湧き出しのあ る水の流れを考えることであった。それは、原点に水の湧き出しがあり、3次 元空間に水が満たされている場合を考えた。ここで、議論する空間は等方的と 仮定するので、立体角$4\pi$[sr]に等しく湧き出しから流出している。

単位時間あたり質量$M$の湧き出しがある場合を考える。$\Delta t$の時間の 湧き出しと、それを含むある閉じた面からの流出量は等しいので、

$$\begin{aligned} M\Delta t &= d \Delta V\\ &=d\Delta t\int \boldsymbol{v}\cdot d\boldsymbol{S} \end{aligned}$$

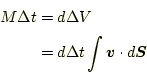が成り立つ。ここで、$d$は水の密度、$\Delta V$は湧き出しを含む任意の閉 じた面での$\Delta t$時間あたりの流出体積、最後はその面での積分である。 この式は、閉じていれば任意の形の面で成り立つのは明らかであろう。これは、 非圧縮性流体の質量保存則に他ならない。この式は、両辺に$\Delta t$があり、 厄介なので、

$$M=d\int \boldsymbol{v}\cdot d\boldsymbol{S}$$ (2)

としておく。

これは、任意の形で成り立つので、湧き出しがある原点を中心とした。半径 $r$の球面を考える。この場合、半径$r$での速度の大きさは全て同じで、その 方向は位置ベクトル $\boldsymbol{r}$なので積分は容易に実行でき、式 (2)は

$$M=dv\times 4\pi r^2$$ (3)

となる。これから、速度は

$$v=\frac{M}{4\pi dr^2}$$ (4)

となる。速度はベクトルなので、もう少し丁寧に書くと、

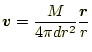$$\boldsymbol{v}=\frac{M}{4\pi dr^2}\frac{\boldsymbol{r}}{r}$$ (5)

となる。この式は、以前見たクーロンの法則から導かれる電場の式

$$\boldsymbol{E}=\frac{Q}{4\pi\varepsilon_0r^2}\frac{\boldsymbol{r}}{r}$$ (6)

と全く同じ形をしている。すなわち、距離の逆2乗則である。

同じ形の式は、全く同じ内容を含む。このことは極めて重要で、諸君は生涯忘 れてはならない。したがって、式(2)に対応するクー ロンの法則は、

$$Q=\varepsilon \int \boldsymbol{E}\cdot d\boldsymbol{S}$$ (7)

となる。クーロンの法則は、教科書の式(1.1)のように書いても良いし、ここ の式(6)でも良いし、式(7)でも良 い。記述の仕方が違うだけで、どれも同じ内容である。全て、電場(力)の大き さは距離の逆2乗に比例すると言っている。その方向についても、3つの式は同 じ内容である。

2.1.2 微小領域での話

次に、微小領域での水の流れ(ベクトル場 $\boldsymbol{v}$)の話をした。微小領域 $\delta x\times\delta y\times\delta z$での流速ベクトル場 $\boldsymbol{v}(x,y,z)$と湧き出しの関係について説明した。この微小領域に、$M$と いう湧き出しがある。その場合、式(2)に対応するものは

$$\begin{aligned} M&=d\left[ \left\{v_x(\delta x,0,0)-v_x(0,0,0... ..._z}{\partial z} \right)\delta x \delta y \delta z \end{aligned}$$

である。無論、この式は $\delta x\rightarrow 0$の極限でのみ正確なのは言 うまでも無い。この式の右辺の微分については、諸君は学習済みで発散 (divergence)と呼ばれる量で、

$$M=d\nabla\cdot\boldsymbol{v}\delta x \delta y \delta z$$ (9)

と書くことができることは知っているだろう。 $\delta x \delta y \delta z$ は微小領域の体積である。単位堆積あたりの湧き出しを$m$と書くと、

$$m=d\nabla\cdot\boldsymbol{v}$$ (10)

と書き直すことができる。ここで、$m$は単位体積あたりの湧き出しを示すス カラー場である。先も言ったように、流体の流れの式とクーロンの法則の式は 同じなので、この式に対応するクーロンの法則もある。それは、

$$\rho=\varepsilon \nabla\cdot\boldsymbol{E}$$ (11)

である。$\rho$は単位体積あたりの電荷量、すなわち電荷密度でありスカラー 場である。この式も、クーロンの法則である。いろいろとクーロンの法則は書 き方があるが、この書き方が最も簡単で私は好きである。この式が示す物理的 内容はクーロンの法則そのものであるが、この式はガウスの法則と呼ばれてい る。私は理由は知らない。

2.1.3 ガウスの発散定理

式(11)を体積積分してみよう。左辺は、電荷密度の体積 積分であるから、その中の電荷量の総和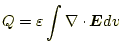$Q$に相当する。したがって、

$$Q=\varepsilon \int \nabla\cdot\boldsymbol{E}dv$$ (12)

である。

この式の右辺は、発散の積分である。小さい領域を流量の出入りを足し合わせ ている。隣り合う領域では、同じ境界面を共有し、その出入りの総和はゼロで ある。したがって、全体の積分は、その体積の表面での出入りの総和に他なら ない。式であらわすと、

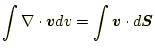$$\int \nabla\cdot \boldsymbol{v}dv=\int \boldsymbol{v}\cdot d\boldsymbol{S}$$ (13)

である。これもおなじみのガウスの発散定理である。 したがって、

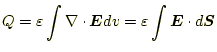$$Q=\varepsilon \int \nabla\cdot\boldsymbol{E}dv=\varepsilon \int \boldsymbol{E}\cdot d\boldsymbol{S}$$ (14)

となる。実際、いろいろな式が出てきたが、憶えておくべき式は、

$$\nabla\cdot\boldsymbol{E}=\frac{\rho}{\varepsilon}$$ (15)

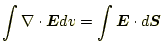$$\int \nabla\cdot\boldsymbol{E}dv=\int \boldsymbol{E}\cdot d\boldsymbol{S}$$ (16)

の2つである。最初の式は4つあるMaxwellの方程式の一つで、2つめのものはガ ウスの発散定理である。

2.2 先週の補足

式(8)の求め方に疑問を持つ人がいるであろう。もう少し 一般的にしよう。yz平面での速度ベクトル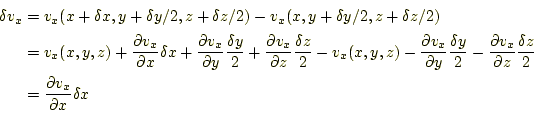$v_x$の差は

$$\begin{aligned} \delta v_x &=v_x(x+\delta x,y+\delta y/2,z+\d... ...}{2}\\ &=\frac{\partial v_x}{\partial x}\delta x \end{aligned}$$

となる。これと同じ事を、zx面とxy面で行い、全ての面を足し合わせれば、式 (8)と同じ結果が得られる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志