1 ベクトル解析の演習問題
1.1 ベクトルの演算
- まずは、小手調べとして、次のベクトルの和
(
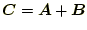 )と差(
)と差(
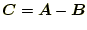 )
を計算せよ。ただし、和と差は2通りの方法、
)
を計算せよ。ただし、和と差は2通りの方法、
- 成分同士の和を計算する方法。
- 図形により、ベクトルをつなぐ方法。
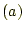



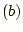


-
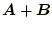 と
と
 が与えられているとき、
が与えられているとき、
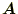 と
と
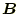 はどのようにすれば求められるか?
はどのようにすれば求められるか?
-
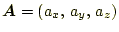 、
、
 の時、
の時、
 と
と
 を示せ。
を示せ。
-
 、
、
 のとき、内積
(
のとき、内積
(
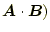 と外積
と外積
 および
(
および
(
 を計算せよ。
を計算せよ。
-
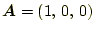 、
、
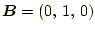 のとき、内積
のとき、内積
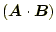 と外積
と外積
 および
および
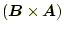 を計算せよ。
を計算せよ。
-
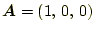 、
、
 のとき、内積
のとき、内積
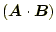 と外積
と外積
 および
および
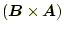 を計算せよ。
を計算せよ。
- 位置ベクトル
 の各成分を示せ。
の各成分を示せ。
1.2 微分
- スカラー場
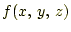 があるとき、その勾配
があるとき、その勾配 の各成分を
示せ。
の各成分を
示せ。
- 位置ベクトル
 の大きさの勾配を示せ。
の大きさの勾配を示せ。
-
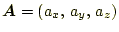 の時、
の時、
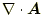 と
と
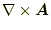 を示せ。
を示せ。
- 以下を確認せよ。
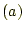


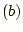
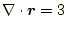

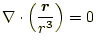

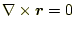
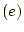
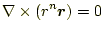
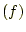

- 次のベクトル場は、図5〜
10のどれに対応するか分かるか?。ただし、分
かりやすくするために、ベクトルの大きさはスケールされている。



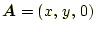

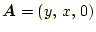

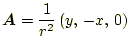
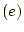
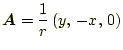
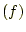
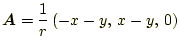
- 図5〜10のうち、
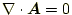 あるは
あるは
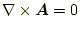 のものはどれか?。
まずは、計算をしないで考えよ。その後、計算を行い確認せよ。
のものはどれか?。
まずは、計算をしないで考えよ。その後、計算を行い確認せよ。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月28日
![\includegraphics[keepaspectratio, scale=0.7]{figure/grid.eps}](img28.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/fig1.eps}](img51.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/fig2.eps}](img52.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/fig3.eps}](img53.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/fig4.eps}](img54.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/fig5.eps}](img55.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/fig6.eps}](img56.png)