3 倍精度実数のいろいろな誤差

倍精度実数型(double)のいろいろな誤差を，実際のプログラムで体験してもらう．

3.1 丸め誤差

先程述べたように，実数は有限のビット数で表現されるため，2進数での桁数が無限に必 要な場合はメモリー中のデータには誤差が含まれる．この誤差を丸め誤差(rounding error)と 言う．以下のプログラムを実行して，それを確認せよ．

9行

%80.75fは80カラム用意して，小数点以下75桁で表示せよという意味．

   1 #include <stdio.h>
   2 
   3 int main(void){
   4 
   5   double x;
   6 
   7   x=0.3;
   8 
   9   printf("%80.75f\n",x);
  10 
  11   return 0;
  12 }

練習問題

[練習1]

リスト2を書き換えて，誤差が生じ ない例を探せ．

[練習1]

倍精度実数型で1以上の整数の場合はどうなるか?．プログラ ムを書き換えて調べよ．

3.2 情報落ち

倍精度実数型の精度は，およそ $(2^{-54})=5.5\times 10^{-17}$ と先ほど述べた．この精 度よりも大きさの差(絶対値)が小さい2つの実数の和と差の演算はできない．このことを 以下のプログラムで確認する．zの値は，xの値に1000000回yの値を加算 するプログラムとなっている．すなわち，

$$z=x+1000000y$$ (5)

である．計算結果がどうなるか確認せよ．

   1 #include <stdio.h>
   2 
   3 int main(void){
   4 
   5   double x, y, z;
   6   int i;
   7 
   8   x=1.0;
   9   y=1e-17;
  10 
  11   printf("%80.75f\n",x);
  12   printf("%80.75f\n",y);
  13 
  14 
  15   z=x;
  16   for(i=1;i<=1000000;i++){
  17     z+=y;
  18   }
  19 
  20   printf("%80.75f\n",z);
  21 
  22   return 0;
  23 }

練習問題

[練習1]

リスト3を書き換えて，誤差が生じ ない例を探せ．

[練習2]

積や商の場合はどうか?．調べよ．

3.3 打ち切り誤差

三角関数を計算する場合，以下のような級数を使う．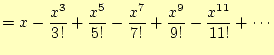

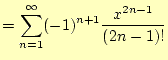$$\sin x =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!} -\frac{x^{11}}{11!}+\cdots$$

$$=\sum_{n=1}^{\infty}(-1)^{n+1}\frac{x^{2n-1}}{(2n-1)!}$$ (6)

コンピューターでは無限級数を計算することはできない．これをきちんと計算するために は，無限界の計算回数が必要で，無限の時間がかかる．それに，精度が有限であるため， ある程度以下の計算は無意味である．そのため，精度内に計算が収まったら，計算を止め るようになっている．途中で計算を打ち切るので，この誤差を打ち切り誤差と言う．

ホームページ: Yamamoto's laboratory
著者: 山本昌志