2 ソートのアルゴリズム

ソートとは，データをある規則にしたがい順番に並び替えることである．ここでは，ランダムに並んだ整数(数列)を昇順に並び替えることを学習した．

2.1 バブルソート

2.1.1 原理

数列の隣どうしの要素の大小を比較してそれらを交換しながらソートする方法である．交換が1回も生じなかったら，ソートが完了である．これは，小さい値のデータが泡(バブル； bubble)のように浮かんで行くように見える²ことからこの名前がつけられた．

リスト1が配列sortに格納された整数を昇順に並び替えるプログラムである．このプログラムの動作を考えるために，データ数をNとして， sort[0]を左端，sort[N]を右端とする．すると，以下のことが分かる．

もっとも値の大きいデータは，外側の1回のループ(5行目のdo)で右端に移動する．
左に移動すべき小さいデータは，このループで一つずつしか移動できない．この一つずつしか移動できないので，整列に多くの計算回数が必要となる．

このプログラムでは，doループ中の11行目の

	if(sort[i]>sort[i+1])

がもっとも多く実行される文である．この文の最小実行回数は，最初から整列できている場合である．このときの，実行回数は，

回であるのは明らかである．最悪の場合は，最小の値が右端にある場合である．この場合の実行回数は，

となる．なぜならば，

この最小の値は，1回外側のループ(do文のところ)を実行する毎に，一つ左に移動する．
所定の位置に移動するために，回，外側のループを実行する必要がある．
外側のループを1回実行する毎に，内側のループは回，実行される．

となるからである．

最初のデータの並び方により，回からまで開きがある．初期位置と整列終了位置との差の最大の期待値を計算することになるが，それは程度であることは分かるだろう．最小値の初期位置と整列終了位置との差の期待値である．この程度とすると，先の比較の実行回数は，

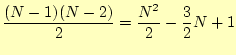$\displaystyle \frac{(N-1)(N-2)}{2}=\frac{N^2}{2}-\frac{3}{2}N+1$

(1)

となる．データ数

が大きい場合，

に比例して計算量が増加する．

このに比例して計算量が必要な場合，と書く．この表記法を記法( -notation)といい，計算オーダーを示す．数学で使うランダウの記号に似ている．バブルソートの計算のオーダーは，である．

2.1.2 プログラム

教科書のList 1-1(p.3-4)のバブルソートの関数は，リスト1の通りである．これをmain関数から呼び出すことにより，配列sortに格納された整数が昇順に並び替えられる．

配列sortはグローバル変数³なので，関数の引数として渡していない．
数列の個数Nは，#defineで与えられる．
入れ替えが生じると，flagの値が1になる．入れ替えが起きないときは， flagの値は0である．これはフラグ(flag:旗)と呼ばれるもので，計算の状態を表す．

リスト1 バブルソートの関数(転載について)

   1 void BubbleSort(void)
   2 {
   3     int     i,j,flag;
   4 
   5     do
   6     {
   7         flag=0;
   8         for(i=0;i<N-1;i++)
   9         /* 先頭から順に見ていって */
  10         {
  11             if(sort[i]>sort[i+1])
  12             /* 左右の並びがおかしければ */
  13             {
  14                 /* 入れ替える */
  15                 flag=1;
  16                 j=sort[i];
  17                 sort[i]=sort[i+1];
  18                 sort[i+1]=j;
  19             }
  20         }
  21         /* 1度も並べ替えをせずに見終わったら終了 */
  22     }   while(flag==1);
  23 }

2.2 クイックソート

2.2.1 原理

ある一つの要素を基準とし基準値より大きいグループと小さいグループに分ける．分けられたグループも同様の方法で分ける．全てのグループの要素が1つになるまでこの作業を繰りかえし，このときソートが完了する．いろいろなソートの中で，平均的には最速であるから，この名前がついている．

2.2.2 プログラム

教科書のList 1-3(p.8-9)のクイックソートの関数は，リスト2の通りである．これをmain関数から呼び出すことにより，配列dataに格納された整数が昇順に並び替えられる．

関数の引数は，ソートする配列の両端(bottom, top)と配列を表すポインター (*data)である．
配列のポインター(*data)は，配列名として使える．

リスト2 クイックソートの関数(転載について)

   1 void QuickSort(int bottom,int top,int *data)
   2 {
   3     int lower,upper,div,temp;
   4     if(bottom>=top)
   5         return;
   6     /* 先頭の値を「適当な値」とする */
   7     div=data[bottom];
   8     for(lower=bottom,upper=top;lower<upper;)
   9     {
  10         while(lower<=upper&&data[lower]<=div)
  11             lower++;
  12         while(lower<=upper&&data[upper]>div)
  13             upper--;
  14         if(lower<upper)
  15         {
  16             temp=data[lower];
  17             data[lower]=data[upper];
  18             data[upper]=temp;
  19         }
  20     }
  21     /* 最初に選択した値を中央に移動する */
  22     temp=data[bottom];
  23     data[bottom]=data[upper];
  24     data[upper]=temp;
  25 
  26     QuickSort(bottom,upper-1,data);
  27     QuickSort(upper+1,top,data);
  28 }

2.3 マージソート

2.3.1 原理

最初に少ない個数の数列を並べ替えたグループを作る．次に，2つのグループを併合(マージ)して，より大きな並び替えられたグループを作る．これを繰り返すことにより，大きなグループができ，最終的には一つのグループになり並び替えが終了する．

2.3.2 プログラム

リスト3 マージソートの関数(転載について)

   1 void MergeSort(int n,int x[])
   2 {
   3     int     i,j,k,m;
   4     if(n<=1)
   5         return;
   6     m=n/2;
   7 
   8     /* ブロックを前半と後半に分ける */
   9     MergeSort(m,x);
  10     MergeSort(n-m,x+m);
  11 
  12     /* 併合（マージ）操作 */
  13     for(i=0;i<m;++i)
  14         buffer[i]=x[i];
  15     j=m;
  16     i=k=0;
  17     while(i<m&&j<n)
  18     {
  19         if(buffer[i]<=x[j])
  20             x[k++]=buffer[i++];
  21         else
  22             x[k++]=x[j++];
  23     }
  24     while(i<m)
  25         x[k++]=buffer[i++];
  26 }

2.4 コームソート

2.4.1 原理

バブルソートは隣との比較のため，小さい値は一つずつしか移動できない(昇順)．比較する間隔を広くして，一気に移動させる方法がコームソートである．このソートでは，適当な間隔でバブルソートを行い徐々にその間隔を狭める方法がとられる．実験から，間隔は

ずつ小さくしていくのが良いと言われている．最終的には隣との比較(間隔が1)を行い，交換が起こらなければソートの完了である．

2.4.2 プログラム

リスト4 コームソートの関数(転載について)

   1 void CombSort(void)
   2 {
   3     int i,temp,flag,gap;
   4     gap=N;
   5 
   6     do
   7     {
   8         gap=(gap*10)/13;
   9         /* 収縮率は1.3（gapが毎回1/1.3になる） */
  10         if (gap==0)
  11             gap=1;
  12 
  13         flag=1;
  14         /* 先頭から順に見ていって */
  15         for (i=0; i<N-gap; ++i)
  16         {
  17             /* 距離がgapだけ離れた要素を比較し，
  18                 並びがおかしければ */
  19             if (sort[i]>sort[i+gap])
  20             {
  21                 /* 入れ替える */
  22                 flag=0;
  23                 temp=sort[i];
  24                 sort[i]=sort[i+gap];
  25                 sort[i+gap]=temp;
  26             }
  27         }
  28 
  29     /* 1度も並べ替えをせずに，gap=1で見終わったら終了 */
  30     }   while((gap>1) || flag!=1);
  31 }

2.5 単純挿入ソート

2.5.1 原理

まず，最初の数列の2つを比較して，小さいほうを左に，大きいほうを右にする．次に数列の3番目を，その左にある2つの数列と小さいほうから順に比較し，収まる位置を探索して，挿入する．これを，4番目,5番目， $\cdots$ と順次，数列の最後まで繰り返す．最後の数列が挿入されたらソートが完了である．

2.5.2 プログラム

リスト5 単純挿入ソートの関数(転載について)

   1 void InsertSort(void)
   2 {
   3     int i,sorted,temp,insert;
   4 
   5     /* 最初から最後まですべてソート済みになるまで繰り返す */
   6     for(sorted=0; sorted<N-1; ++sorted)
   7     {
   8         /* ソート済み領域の直後の値を取り出す */
   9         insert=sort[sorted+1];
  10 
  11         /* 挿入する場所を見つける（リニアサーチ） */
  12         for(i=0; i<=sorted; ++i)
  13             if(sort[i]>insert)
  14                 break;
  15 
  16         /* ソート済み領域直後の値を挿入する */
  17         while(i<=sorted+1)
  18         {
  19             temp=sort[i];
  20             sort[i]=insert;
  21             insert=temp;
  22             ++i;
  23         }
  24     }
  25 }

   1 void BinaryInsertSort(void)
   2 {
   3     int i,sorted,temp,insert;
   4     int left,mid,right; /* バイナリサーチ用の追加変数 */
   5 
   6     /* 最初から最後まですべてソート済みになるまで繰り返す */
   7     for(sorted=1; sorted<N; ++sorted)
   8     {
   9         /* ソート済み領域の直後の値を取り出す */
  10         insert=sort[sorted];
  11 
  12         /* 挿入する場所を見つける（バイナリサーチ） */
  13         left=0;
  14         right=sorted;
  15         while(left<right)
  16         {
  17             mid=(left+right)/2;
  18 
  19             if(sort[mid]<insert)
  20                 left=mid+1;
  21             else
  22                 right=mid;
  23         }
  24         i=left;
  25 
  26         /* ソート済み領域直後の値を挿入する
  27             （単純挿入ソートと同じ） */
  28         while(i<=sorted)
  29         {
  30             temp=sort[i];
  31             sort[i]=insert;
  32             insert=temp;
  33             ++i;
  34         }
  35     }
  36 }

2.7 ソートのアルゴリズムの比較

ソートのアルゴリズムの評価に計算量の他に，安定性というものが使われる．

安定なソートとは，同じ要素があったとき，それらを入れ替えない．
不安定なソートとは，同じ要素があったとき．それらを入れ替える可能性がある．

これら学習したソートの計算量と安定性については，表 1(教科書の Table 1-2)のとおりである．

**表 1:** ソートのアルゴリズムの特徴
アルゴリズム	計算量オーダー	安定性
バブルソート		安定
クイックソート	$O(N\log N)$ ～	不安定
マージソート	$O(N\log N)$	安定
コームソート	$O(N\log N)$	不安定
単純挿入ソート		安定
2分挿入ソート		安定

[転載について]
このページ中のリスト1とリスト2，リスト3,リスト4,リスト5,リスト6のプログラムは，教科書として使用している以下の書籍

書名プログラミングの宝箱　アルゴリズムとデータ構造 ISBN4-7973-2419-8

著作者紀平拓男・春日伸弥

出版社ソフトバンク　パブリッシング株式会社

から転載しました．この転載に関しては，著者と版元に許諾を得ています．

[Previous: 1 アルゴリズムとデータ構造] [Up: これまでの復習(後期中間試験に向けて)] [Next: 3 サーチのアルゴリズム]
[Top:ページの先頭に戻る]

ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
2005-11-28

no counter