Subsections
3 [例題5]シフト演算
教科書のList 5-5のプログラムを例にして,シフト演算を使ったかけ算と割り算の方法を学習する. 以下のことが,ここでの学習の重要なポイントである. -5pt- データを
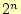 倍するためには,データのビットをシフトさせることにより可能で
ある.
倍するためには,データのビットをシフトさせることにより可能で
ある.
- これを上手に使うと任意のかけ算と割り算ができる.
3.1 積の演算
積(かけざん)の演算を行うとき,シフト命令を使えば効率の良いプログラムができる.ビッ トシフトを用いると積の演算ができる理由は以前述べているが,忘れた人もいるので,も う一度,説明する.
シフト命令を使った積の演算は,小学生のときに学習をした筆算の掛け算と同じである.
たとえば,
![]() を計算する場合,筆算は
を計算する場合,筆算は
![]() と分解したはずである.そうして,次の手順
でこの計算を行ったはずである.
-3pt
と分解したはずである.そうして,次の手順
でこの計算を行ったはずである.
-3pt
 を計算し,1桁ずらす(10倍する).
を計算し,1桁ずらす(10倍する).
 を計算する.
を計算する.
- 先の計算結果を合計する.この合計816が
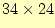 の計算結果である.
の計算結果である.
同じことを2進数で行う.これがコンピューターによる乗算である.先ほどと
同じ計算(
![]() )を行う.これを2進数で表現すると,
)を行う.これを2進数で表現すると,
となる.これを先ほど同様の手順で計算する. -3pt
- 掛け算は1倍なので計算する必要が無く,最初に
 を4桁左
にずらす(ビットシフト).すると,
を4桁左
にずらす(ビットシフト).すると,
 となる.
となる.
- 次に
 を3桁左にずらす.すると,
を3桁左にずらす.すると,
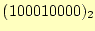 となる.
となる.
- 先の計算結果を合計すると,
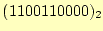 となる.これは,10進
数の816である.
となる.これは,10進
数の816である.
今回の問題のように分数(少数)の場合でも,
| (1) |
と分解する.右に1ビットシフトさせたものと,右に2ビットシフトさせたものを加算すれ ば良い.
教科書のように
| (2) |
と分解するのは一般的ではない.
3.2 プログラムの構造とフローチャート
このプログラムのフローチャートを図3に示す..ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2006-02-14
![\includegraphics[keepaspectratio, scale=0.8]{flow_chart/REI5-5.eps}](img18.png)