5 付録

5.1 コンピューターで2進数が使われる理由

5.1.1 2進数のメリット

人間の指は10本あることは，よく知られている．そのため，人類は10進法を使っていると 言われている．小学校の低学年では指を使って計算する子供がいることからも分かる．コ ンピューターの内部のハードウェアーでは，電圧が0Vか5V(もっと低い場合もある)でデー タやプログラムを表現している．指が2本しかないのと同じ．だから，コンピューターは2 進法を使う．2進法を使うメリットに，何があるか? という疑問が湧くであろう．その答 えとして，以下のようなことが考えられる．

• ノイズに強い

  0〜5Vで動作する素子からできたコンピューターを考える．2ビットと10ビット の場合，割り当てられる電圧のレベルは，図5の通りであ る．図からも分かるように，許されるノイズは，2ビットの方が格段に大きく なる．1ビットのエラーも許されないデジタルコンピューターにおいては，こ の差は非常に大きい．

• ハードウェアーを実現するのが容易

  コンピューター内部には，単純な動作をする同じような部品が数多くある．2進数であれ ば，入力は0と1，出力も0と1なので，構成する1個の部品が非常に単純になる．要するに 2進数を採用すると，部品が簡単になるのである．

• 演算が簡単

  例えば，掛け算九九を考えると分かる．10進数だと，0〜9までの掛け算，合計100通りあ る．2進数だと，4通りで済む．

• ブール代数が使えて，論理演算が容易

  ブール代数については，他の授業で勉強することになっている．それまで待て ない人は，私の講義ノートでも見ろ．

図 5: 2進法と10進法のコンピューターのノイズレベル

5.1.2 2進数のデメリット

それでは，2進数のデメリットとはどのようなことが考えられるであろうか?．すぐに分か ることは，桁数が多くなることである．例えば，十進法の$(99)_{10}$は，二進法では $(1100011)_2$となる．十進法であれば2桁で済むのに，2進法であれば7桁も必要になる．

このことは，コンピューターが発明された当初問題とされたが，すぐにこれは間違いだと 気づく．ある正の整数$k$をそれぞれの位取記数法で表した場合，その底の数$\alpha$と 桁数$\beta$を表2にしめす．$n$進数の場合，整数$k$ を表すの必要な桁数$\log_n k$は次のようにして理解できる．$n$進数が$\beta$桁あると， それが表すことができる組み合わせの数は，$n^\beta$となる．これが，s整数$k$まで表す ことができるから，

$$n^\beta=k$$ (12)

となる．したがって，必要な桁数は，

$$\beta=\log_n k$$ (13)

となる．

表 2: 整数$k$を表すときの底と桁数

底の数$\alpha$	桁数$\beta$
1	$k$
n	$\log_n k$
k	1

それでは，一番効率のよい底の数はいくつであろうか?．効率の定義はいろいろ出来るが， ここでは

• 底の数と桁数で評価することにする．ある整数を表す場合，これらの数の合計が 小さいことが，効率がよい．

とする．$n$進数で正の整数$k$を表す場合，効率は，

$$\alpha+\beta=n+\log_n k$$ (14)

となる．これが最小となるのは，$n$で微分したときゼロとなる，

$$\frac{\mathrm{d}(\alpha+\beta)}{\mathrm{d}n} =1-\frac{\log k}{n(\log n)^2}$$

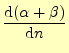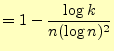$$=0$$ (15)

である．この方程式の解，すなわちもっとも効率の良い底を図6に示 す．この図から分かるように，比較的小さな数字($\leq 10^5$)では4進数あたりが効率が よい．大きな数になると10進数程度が最適な底となる．コンピューターが扱う最大の数は， 大体$2^{32}$程度⁴である．これだと，2進数で32桁，10進 数で10桁である．この場合，図から分かるようにもっとも効率の良いのが6進数であるが， これだと，13桁が必要である．2進数，6進数，10進数をつかっても，桁数は10〜32 である．コンピューターにとって，32桁を取り扱うことは簡単なことなので，2進数で数 字を表現しても全く問題ない．10進数をつかうことに比べて3倍程度の桁数の増加にしか すぎないのである．2進数を使うことによる桁数の増加は，さほど大きなデメリットではない． それよりも，2進数を使うメリットの方が圧倒的に多い．

図 6: もっとも効率の良い底．横軸は整数で，縦軸はその整数を表すときのもっと も効率の良い底．

5.2 少数の表現(おまけ)

5.2.1 位取り記数法

10進数での小数の表現を考える。例えば，小数の表現，

$$(0.1235)_{10} =(1\times 10^{-1}+2\times 10^{-2}+3\times 10^{-3}+5\times 10^{-4})$$ (16)

　　 と整数の場合と同じようになっている。小数点を境に、右側の指数部が-1, -2, -3と1ず つ減少する。これは、先に示した整数の場合と全く同じで，簡単である。当然，

$$10^{-1}=\frac{1}{10^1}=\frac{1}{10}=0.1$$

$$10^{-2}=\frac{1}{10^2}=\frac{1}{100}=0.01$$

$$10^{-3}=\frac{1}{10^3}=\frac{1}{1000}=0.001$$

$$\qquad\vdots$$

$$10^{-N}=\frac{1}{10^N}$$ (17)

は理解していなくてはならない．

5.2.2 基数の変換(2進数 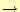$\rightarrow$10進数)

2進数での少数の表記も、10進数の場合と同じである。だから、2進数少数を10進数少数に 変換するのは簡単である。たとえば、

$$(0.10101)_2 =(1\times 10^{-1}+0\times 10^{-10}+1\times 10^{-11}+ 0\times 10^{-100}+1\times 10^{-101})_2$$

$$=(1\times 2^{-1}+0\times 2^{-2}+1\times 2^{-3}+ 0\times 2^{-4}+1\times 2^{-5})_{10}$$

$$=(1\times 0.5+0\times 0.25+1\times 0.125+ 0\times 0.0625+1\times 0.03125)_{10}$$

$$=(0.5+0.125+0.03125)_{10}$$

$$=(0.65625)_{10}$$ (18)

となる．当然

$$2^{-1}=\frac{1}{2^1}=\frac{1}{2}=0.5$$

$$2^{-2}=\frac{1}{2^2}=\frac{1}{4}=0.25$$

$$2^{-3}=\frac{1}{2^3}=\frac{1}{8}=0.125$$

$$\qquad\vdots$$

$$2^{-N}=\frac{1}{2^N}$$ (19)

は理解していなくてはならない．

5.2.3 基数の変換(10進数 $\rightarrow$2進数)

つぎは，先ほどと逆を考える．たとえば，先ほどの例の $(0.65625)_{10}$を2進数で表現 する．そのためには，

$$(0.65625)_{10} =(a_1\times 2^{-1}+a_2\times 2^{-2}+a_3\times 2^{-3}+\cdots)_{10}$$ (20)

と書き直せばよい．ただし，$a_n$は0または1である．そして，この$a_n$を並べると，

$$(0.65625)_{10}=(a_1a_2a_3\cdots a_4)_2$$ (21)

と2進数で表現できる．ここで，問題は$a_n$を求めることである．そこで，式 20の両辺を2倍する．すると，

$$(1.3125)_{10} =(a_1\times 2^{0}+a_2\times 2^{-1}+a_3\times 2^{-2}+\cdots)_{10}$$ (22)

となる．この式の両辺の整数部と小数部は等しいので，

$$(1)_{10}=(a_1)_{10} (0.3125)_{10} =(a_1\times 2^{0}+a_2\times 2^{-1}+a_3\times 2^{-2}+\cdots)_{10}$$ (23)

となる．これで，$a_1=1$が求まった．同じように，残りの小数部分を2倍すると，

$$(0.625)_{10} =(a_2\times 2^{0}+a_3\times 2^{-1}+a_4\times 2^{-2}+\cdots)_{10}$$ (24)

となる．これも，両辺の整数部と小数部が等しいので，

$$(0)_{10}=(a_2)_{10} (0.625)_10=(a_3\times 2^{-1}+a_4\times 2^{-2}+a_5\times 2^{-3}+\cdots)_{10}$$ (25)

が得られる．これで，$a_2=0$が求まった．同様に以下の通り，残りの小数部分の計算を進める と，全ての$a_n$が求まる．

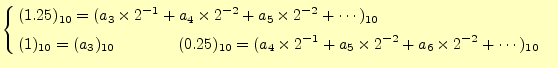$$\left\{ \begin{aligned}&(1.25)_{10} =(a_3\times 2^{-1}+a_4\times ... ...es 2^{-1}+a_5\times 2^{-2}+a_6\times 2^{-2}+\cdots)_{10}& \end{aligned} \right.$$ (26)

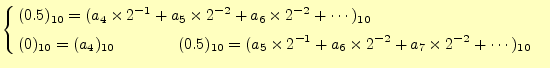$$\left\{ \begin{aligned}&(0.5)_{10} =(a_4\times 2^{-1}+a_5\times 2... ...es 2^{-1}+a_6\times 2^{-2}+a_7\times 2^{-2}+\cdots)_{10}& \end{aligned} \right.$$ (27)

$$\left\{ \begin{aligned}&(1.0)_{10} =(a_5\times 2^{-1}+a_6\times 2... ...es 2^{-1}+a_7\times 2^{-2}+a_8\times 2^{-2}+\cdots)_{10}& \end{aligned} \right.$$ (28)

最後に、小数部がゼロとなったので計算は、完了となる。以上をまとめると

$$(0.65625)_{10} =(a_1\times 2^{-1}+a_2\times 2^{-2}+a_3\times 2^{-3}+\cdots)_10$$

$$=(1\times 2^{-1}+0\times 2^{-2}+1\times 2^{-3}+0\times 2^{-4}+1\times 2^{-5}+)_10$$

$$=(0.10101)_2$$ (29)

となる．要するに、小数部を2倍して、その整数部を書いていけばよい．

よく使われるのは、図7のようにして計算を進める．2倍して，整数部を書 き出して，小数部を再度2倍する．これを繰り返すと，10進数小数を2進数小数に変換する ことができる．10進数の0.1は循環小数ではないが、2進数にすると、

$$(0.1)_{10}=(0.00011001100110011\cdots)_2$$ (30)

と循環小数になる．通常は，途中まで(必要な精度まで)で，計算を打ち切る．

図 7: 小数の基数変換(10進数 $\rightarrow$2進数)

ホームページ: Yamamoto's laboratory
著者: 山本昌志