4 負の数の表現
- COMET IIでは,負の整数は2の補数で表現されます.メモリーの中に, 16ビットで格納されます.
- 負の数を2の補数で表現する手順は,以下の通りです.
- 120D
- 負の数の絶対値を2進数で表現して,ビット反転する.
- 220D
- +1加算
- [例]
-
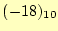 は,COMET IIの内部,16ビットの2の補数は,
は,COMET IIの内部,16ビットの2の補数は,
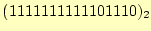 と表されます(メモリーへの格納状
態).
と表されます(メモリーへの格納状
態).
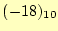
0000000000010010 
18の2進数表現(16ビット) 1111111111101101 
ビット反転 1111111111101110 
+1加算 - 2の補数を使うと,以下の有利な点があります.
- 負の数の加算が通常の加算器で出来る.
- 加算の場合の負の数,あるいは減算は,120D2の補数に変換 して,220D加算器による加算を行う.減算器を作るより,こ の方が回路が簡単になる.
- 2の補数を求める手順(120Dビット反転 220D+1加算)は,コン
ピューター内部表現では,
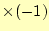 と同じです.
と同じです.
- COMET IIの符号付き整数
- 正の数は16ビット2進数でそのままの表現です.一方,負の数は 2の補数を使います.正か負かの判断は,最上位のビットで判断 します.最上位の第15ビットが0ならば正,1であれば負です.
- 最上位のビットが符号を表すため,絶対値は残りのビットで表
すことになります.したがって,表現可能な整数は-32768〜
32767です.
正の整数の最大値 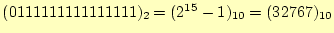
負の整数の絶対値の最大値 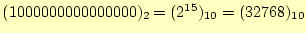
- COMET IIの符号無し整数
- 正の数は16ビット2進数でそのままの表現です.一方,負の数を 表すことはできません.
- 正の整数は,16ビットのパターンが2進数と同じです.したがっ
て,表現可能な整数は0〜65535です.
最小値 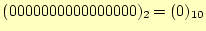
最大値 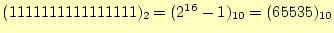
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2005-11-25
![\includegraphics[keepaspectratio, scale=1.0]{figure/hosuukeisan.eps}](img25.png)