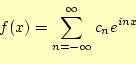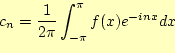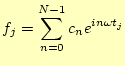2 原理
2.1 フーリエ級数(実数)
「電気回路」の授業で学んだように,正弦波以外の波形の交流を「ひずみ波交流」と言う.波形のひずみ(正弦波からのひずみ)が少ないときには,これと等価な正弦波として取り扱うことができるが,ひずみ波の度合いが大きいとそのような取り扱いはできない.図1に示すように,ひずみ波は周波数の異なった複数の正弦波が重なったものと考え られる.
一般に,変数![]() の関数
の関数![]() が
が![]() の周期をもつ周期関数であるとき,すなわち
の周期をもつ周期関数であるとき,すなわち
![]() であるときは,
であるときは,![]() は
は
![$\displaystyle =\frac{a_0}{2}+\sum_{n=1}^{\infty}\left[a_n\cos nx+b_n\sin nx\right]$](img12.png) |
(1) |
とフーリエ級数に展開することができる.ここでは,関数や変数,あるいは係数の全ては,実数である.
ここで,時間![]() の関数の場合を考える.独立変数が
の関数の場合を考える.独立変数が![]() になり,関数
になり,関数![]() は周期
は周期![]() の周期関数とする.関数が
の周期関数とする.関数が![]() の周期を持つためには,
の周期を持つためには,
 |
(2) |
という形になる.独立変数は,
と書き表すことができる.もう少し変形すると,
と記述しても,同じである.ただし,
| (4) |
である.ここで,
ここで,![]() や
や![]() を求めることにが残された問題である.通常,それらを直接求めるのではなく,フーリエ係数
を求めることにが残された問題である.通常,それらを直接求めるのではなく,フーリエ係数![]() や
や![]() を求めることになる.そのためには,三角関数が直交関数であること
を求めることになる.そのためには,三角関数が直交関数であること
 |
(5) | |
 |
(6) | |
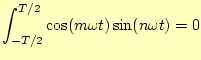 |
(7) |
や,その他の性質
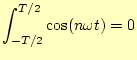 |
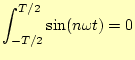 |
(8) |
を使うことになる.ただし,
が得られる.これで,任意の周期関数を三角関数で展開するとき,必要な情報の全てが得られたことになる.
2.2 複素フーリエ級数
これまでは,実数で考えていたが,複素数で考える方が簡単な場合が多い.特に理論的な計算をする場合は,複素数にして取り扱う方が手間が少なくて済む.三角関数を複素数は,オイラーの公式1| (11) |
で結ばれる.したがって,
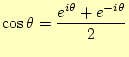 |
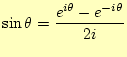 |
(12) |
となる.これを使うと,式(3)は
となる.ここで,
となる.もう一方も,
と似たような式になる.というか,複素共役の関係である.ここで,
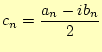 |
(16) |
とおく.すると,(10)と(11)から,
 |
となり,式(15)と(16)とも矛盾しない.同様 に,
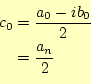 |
となる.これらから,式(14)は,
となる.その係数
と計算できる.これが複素フーリエ級数である.
式(20)は式(3)と同等 であり,式(21)はまた式(10)や式(11)と同等となっている.同等な式であるが,複素数で表し た方が簡素に記述できている.これだけでも複素数を使う価値はある.
2.3 離散フーリエ変換と高速フーリエ変換
実際にデータを測定する場合,それは必ず離散量である.1秒間間に100万回測定しても, それは離散化された量である.この離散化された量のフーリエ係数を求めることが,離散 フーリエ変換や高速フーリエ変換である.ここでは詳しく述べないが,いわゆるフーリエ 変換(フーリエ積分)とは,少しばかり異なる.
ここで,データを取得した間隔を![]() とする.その,期間の中で
とする.その,期間の中で![]() 個
の等間隔でデータがえられたとする.そして,
個
の等間隔でデータがえられたとする.そして,![]() 番目のデータは,
番目のデータは,
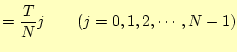 |
(21) |
の時刻にデータが得られたものとする.ここで得られデータを
| (22) |
とする.
実際のフーリエ級数の式(20)
を評価したい.測定量である![]() と
と![]() はそれぞれ
はそれぞれ![]() 個なので,フーリエ係数の
個なので,フーリエ係数の![]() も
独立に
も
独立に![]() 個決めることができる.そうすると展開の基底関数もN個となる.したがってフー
リエ級数の展開式は,
個決めることができる.そうすると展開の基底関数もN個となる.したがってフー
リエ級数の展開式は,
と書くことができる.ここで残された問題は,測定量の
とすることができる.この式が離散フーリエ変換,Discreate Fourier Transform(DFT)と 呼ばれる式である.
式(25)は離散フーリエ変換,式(24)逆変換と呼ば れ,相関関数や周波数スペクトラムなどの時間および周波数領域でのデジタル信号処理の 基礎となるものである.
FFTはDFTの計算で同じ乗算を何回も繰り返すことがないよう,演算手順を合理化したもの
である3.それはデータのサンプル
数![]() が2つ以上の整数
が2つ以上の整数
![]() の積になっているときに可能であり,このと
き通常必要な
の積になっているときに可能であり,このと
き通常必要な![]() の乗算が
の乗算が
![]() 回に短縮される.
回に短縮される.
1965年に米国のCooleyとTukeyによって開発されたFFTのアルゴリズムは,![]() として2
進のデジタル計算に適するようにしたもので,このとき乗算回数は
として2
進のデジタル計算に適するようにしたもので,このとき乗算回数は![]() 回から
回から
![]() 回に短縮された.例えば,
回に短縮された.例えば,![]() の場合に乗算回数が50分の1に短縮され,
の場合に乗算回数が50分の1に短縮され,
![]() が大きいほど短縮の割合が大きくなることが分かっている.
が大きいほど短縮の割合が大きくなることが分かっている.
デジタル信号処理において,かなりの計算時間を要する乗算の回数が大幅に減少するFFT のアルゴリズムの利用によって,周波数スペクトラム分析がデジタル計算機を用いて短時 間で行えるようになった.また,LSI技術の発展に伴って,小型で低価格の専用のFFT周波 数分析装置が開発され,広く利用されている.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年10月21日
![\includegraphics[keepaspectratio,scale=1.0]{figure/FFT/hizumiha.eps}](img5.png)
![$\displaystyle f(t) =\frac{a_0}{2}+\sum_{n=1}^{\infty}\left[a_n\cos(n\omega t)+b_n\sin(n\omega t)\right]$](img20.png)

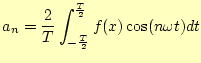
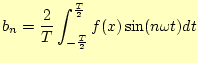
![$\displaystyle f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left[\frac{a_n-ib_n}{2}e^{in\omega t}+\frac{a_n+ib_n}{2}e^{-in\omega t}\right]$](img50.png)