2 原理と実験方法
2.1 論理回路実習装置(ITF-02)を用いた実験
2.1.1 半加算器と全加算器の実習
加算器の理論
加算器には,下位からの桁上げを考慮しない半加算器(Half Adder)と,下位からの桁上 げを考慮する全加算器(Full Adder)がある.全加算器は,半加算器を2個,直列に接続 した形になる.また,後で示すことになるが,回路の和(Sum)を構成している部分は, Exclucive ORになっている.
和(Sum)をS,桁上げ(Carry)をCとすれば,半加算器の真理値表は,表 1のようになる.この真理値表から,半加算器では, 次式のような論理式が得られる.
| (1) | ||
| (2) | ||
| (3) |
となる.または,
| (4) |
と書いても同じである.これらの論理式を論理回路に置き換えると,図 1や2のようになる.
全加算器の真理値表は,表2のようになる.これか ら,その論理式は
| (5) | ||
| (6) | ||
| (7) | ||
| (8) |
となる.いま,
| (9) |
となる.また,
| (10) | ||
| (11) | ||
| (12) |
となり,さらに,Exclucive OR で表せば,
| (13) | ||
| (14) | ||
| (15) |
となる.この論理式は,図3や 4のような論理回路になる.
加算器の実習
図1から図4に示した4つの加算
回路をパネル上で構成し,真理値表を表示器で確認する.実際の実習回路は,図
5から図8に示す.
| A | B | C
|
S | C
|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
2.1.2 エンコーダー(encoder)の実習
エンコーダーの理論
情報を符号化する回路をエンコーダーと言う.ここでは,10進数を4ビットの2進数コー ド(たとえば,BCDコード)にコード化するような論理回路について学習する.10進数と BCDコードの関係は,次のようになる.
| 10進数 | "0"〜"9" |
| 2進数 | A= |
| C= |
として
A="1"+"3"+"5"+"7"+"9"とする.この真理値表を,表3に示す.そして,これ に対応する論理回路を図9に示す.
B="2"+"3"+"6"+"7"
B="4"+"5"+"6"+"7"
B="8"+"9"
エンコーダーの実習
パネル上のエンコーダー部分を使用し,図9の論理回路を作成す
る.図10に接続例を示す.
| 10進 | 2進出力 | |||
| 入力 | D | C | B | A |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
2.1.3 デコーダー(decoder)の実習
デコーダーの理論
符号化された情報を元に戻す回路をデコーダーと言う.ここでは,4ビットの2進数コー ドを,もとの10進数に戻す回路を学習する.
BCDコードでは,2進数と10進数の関係は,次のようになる.
| 2進数コード | A= |
| C= |
|
| 10進数 | "0"〜"9"として |
| "0"=
|
|
| "1"=
|
|
| "2"=
|
|
| "3"=
|
|
| "4"=
|
|
| "5"=
|
|
| "6"=
|
|
| "7"=
|
|
| "8"=
|
|
| "9"=
|
この式を満足する真理値表は,表4の通りである.そ の論理回路は,図11の示すとおりである.
デコーダーの実習
パネル上のデコーダーの部分を使用して,11の論理回路を作成す
る.接続例を図12に示す.
| 2進入力 | 10進出力 | |||||||||||||
| D | C | B | A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
2.2 論理回路実習装置(ITF-07)を用いた実験
2.2.1 累算器を用いた加算回路の実習
加算の理論
2進法による加算方法には,並列加算方式と直列加算方式があるが,本装置では,動 作が分かりやすい直列加算方式を採用している.直列加算方式の基本回路は,図2-2に 示すように被加数レジスタ(A),加数レジスタ(B),加算器桁上げメモリ (C),および和レジスタ(Y)で構成される.
加算の実行は,被加数レジスタ(A),加数レジスタ(B)のデータを下位ビット
から1ビットずつ右へシフトさせ,加算器で加算したデータを和レジスタに,順次入力
する方法でおこなわれる.レジスタのビット数だけのシフトと加算がおこなわれて,演
算が終了する.加算器による加算は,次のようにおこなわれる.例えば,10進数の![]() の場合,この式を4ビットの2進数で書きなおすと次式になる.
の場合,この式を4ビットの2進数で書きなおすと次式になる.
| (16) | ||
| (17) | ||
| (18) | ||
| (19) | ||
加算は(A)(B)の
| (20) | ||
| (21) | ||
| (22) |
| (23) | ||
| (24) | ||
| (25) |
このように,キャリー出力C
図13方式では,レジスタが3個必要であるが,被加数レジス タの空いたビットに加算機の結果を順番に入れていけば,レジスタは2個ですむ.この ように,被加数レジスタと和レジスタを兼ねたレジスタを累算器と言う.
累算器を用いた加算の回路構成を図14に示す.この方式では, 累算(連続の加算)が可能になる.例えば,10進数の1+2+5=8の加算をおこなう場合, 次のような動作となる.
- 累算器の内容を全ビット,ゼロにする.&dotfill#dotfill;00000
- 加数レジスタに,10進数1に相当する2進数を設定する.&dotfill#dotfill;00001
- 加数をおこなう.累算器のデータ&dotfill#dotfill;00001
- 加数レジスタに,10進数2に相当する2進数を設定する.&dotfill#dotfill;00010
- 累算器と加数レジスタの加算をおこなう.
累算器のデータ&dotfill#dotfill;00011 - 加数レジスタに10進数5に相当する2進数を設定する.&dotfill#dotfill;00101
- 累算器と加数レジスタの加算をおこなう.
累算器のデータ&dotfill#dotfill;01000
5ビットのレジスタによる累算の容量は11111で,10進数の31となるので,この範囲まで の累算がおこなえることになる.ただひ,本装置では,10進数変換回路が19までの容量 しかないので,10進数で見る場合は19までとなり,2進数のままであれば5ビット(10進 数の31)フルに見ることができる.
加算の実習- 電源スイッチをOFFにする.
- 端子1と2, 4と18, 6と16, 7と17および10と11間をリードチップで接続する. (図13参照)
- 「A」累算器のシフト方向スイッチを,
 印方向に設定する.
印方向に設定する.
- 「B」
 レジスタの表示器ON/OFFスイッチを,OFFにする.
レジスタの表示器ON/OFFスイッチを,OFFにする.
- 「M」レジスタの表示器ON/OFFスイッチを,OFFにする.
- 10進数表示器ON/OFFスイッチを,左右の2個ともOFFにする.
- 「A」
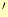 /「A」切換スイッチを「A」側に設定する.
/「A」切換スイッチを「A」側に設定する.
- 電源スイッチをONにし,以下の操作をおこなう.
![]() 操作順序
操作順序
具体的な数値(たとえば7+5=12)を用いて,操作順序を説明する.演算の過程は, 図16に示す. []
- =1pt =0.2pt CLをプッシュして,各レジスタの内容と表示をゼロにする.
- レジスタ選択(A)をプッシュする.
- 数字設定キーの=1pt =0.2pt 7をプッシュする.「A」累算器には,被加数7に 相当する2進数がセットされる.
- レジスタ選択スイッチの(B)をプッシュする.
- 数字設定キーの=1pt =0.2pt 5をプッシュする.「B」レジスタには,加数5に 相当する2進数がセットされる.
- =1pt =0.2pt ADDをプッシュして,「A」累算器と「B」レジスタの最下位ビッ
トどうしの加算をおこなう.S=0, C
 =1となる.
=1となる.
- =1pt =0.2pt Iを1回プッシュして,「A」累算器と「B」レジスタの内容
を,右へ1ビットシフトさせる.S=0のデータは「A」累算器の最上位
ビットに記憶され,C
 =1のデータは桁上げメモリに記憶されて,
C
=1のデータは桁上げメモリに記憶されて,
C
 =1となる.
=1となる.
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=0,
C
 =1となる.
=1となる.
- =1pt =0.2pt Iを1回プッシュして,[7]と同様にシフトさせる.S=0のデー
タは「A」累算器の最上位ビットに記憶され,C
 =1のデー
タは桁上げメモリに記憶されて,C
=1のデー
タは桁上げメモリに記憶されて,C
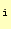 =1となる.
=1となる.
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=1,
C
 =1となる.
=1となる.
- =1pt =0.2pt Iを1回プッシュして,[7]と同様にシフトさせる.S=1のデー
タは「A」累算器の最上位ビットに記憶され,C
 =1のデー
タは桁上げメモリに記憶されて,C
=1のデー
タは桁上げメモリに記憶されて,C
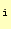 =1となる.
=1となる.
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=1,
C
 =0となる.
=0となる.
- =1pt =0.2pt Iを1回プッシュして,[7]と同様にシフトさせる.S=1のデー
タは「A」累算器の最上位ビットに記憶され,C
 =0のデー
タは桁上げメモリに記憶されて,C
=0のデー
タは桁上げメモリに記憶されて,C
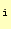 =0となる.
=0となる.
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=0,
C
 =0となる.
=0となる.
- =1pt =0.2pt Iを1回プッシュして,[7]と同様にシフトさせる.S=0のデー
タは「A」累算器の最上位ビットに記憶され,C
 =0のデー
タは桁上げメモリに記憶されて,C
=0のデー
タは桁上げメモリに記憶されて,C
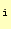 =0となる.以上の操作で,
5ビット全部の演算が終了する.「A」累算器には,演算結果の和
(
=0となる.以上の操作で,
5ビット全部の演算が終了する.「A」累算器には,演算結果の和
( )が記憶されている.
)が記憶されている.
- [15]の2進数データを10進数表示するために,10進数表示器ON/OFFスイッ チの左側のスイッチをONにすると,"12"と表示される.
![]() 注意
注意
- キーをプッシュするときは,1個ずつゆっくりプッシュすること.2個ずつ や,中途半端な操作は誤作動の原因となる.
- 累算をおこなう場合は,まずCP1をリセットする.そのためには,CP1の表 示が"0"になるように,=1pt =0.2pt Iをプッシュする.同様のことが,=1pt =0.2pt II IIIをプッシュすることによってもできる.なお,=1pt =0.2pt CLをプッシュする と,全部の設定がリセットされるので注意すること.
- CP1をリセットしたのち,2.2.1節の"操作順序"の [4]以降を,再度操作すること.累算がおこなわれる.
- "2.2.1 累算器を用いた加算回路の実習"では,累算がお
こなえるように累算器を使用しているが,累算器を被加数レジスタとして加算
をおこなう場合は,次のように設定すること.
- 端子1と2,3と4,6と16,7と17,10と11,18と19および23と25をリードチップで 接続する.
- 「A」累算器のシフト方向スイッチを,
 印方向に設定する.
印方向に設定する.
- 「M」レジスタのシフト方向スイッチを,
 印方向に設定する.
印方向に設定する.
- 「B」
 レジスタの表示器ON/OFFスイッチをOFFにする.
レジスタの表示器ON/OFFスイッチをOFFにする.
- 「M」レジスタの表示器ON/OFFスイッチをONにする.
- 10進数表示器ON/OFFスイッチを左右の2個ともOFFにする.
- 「A」+「M」/「M」切換スイッチを,「M」側に設定する.
- 2.2.1節の"操作順序"の[1]〜[15]をおこなう. ただし,シフトさせたデータが「M」レジスタに入るため,図 16の「A」累算器の表示は,最終的には,「M」 レジスタにあらわれる.
- 「M」レジスタの2進数データを10進数表示するため,10進数表示器ON/OFFスイッ チの右側のスイッチをONにする.
2.2.2 加算回路と補数器を用いた減算回路の実習
減算の理論 減算は,減数の補数と被減数の加算をお こなうことにより実行される.したがって,加算回路に補数器が付け加えられた回路構成 となる.図17に減算の基本回路を,図 18に累算器を用いた減算回路をそれぞれ示す.本装置の補数器 は,2の補数を得るためにまず,入力されたデータを否定回路で反転し,その後,最下位 ビットに1を加える方法を採用している.減算においては,その結果(差)が負数になることもある.正・負の判別は,最上位ビット が1なら負数,0なら正数になる.その様子を表6に示す.た だし,これは"0"〜"9"までを5ビットの2進数で表示した場合で,4ビットで表示したとき は,"0"〜"7"までしか判別できない.累算をしない1桁の減算の場合,最も大きな負数に なるのは0-9=-9なので,5ビット表示が必要である.
累算をおこなう1桁の減算の場合,-15まで負数の判別ができる.表 6に,"0"〜"16" における5ビットの正数と負数の2進数表示 を示する."16"では正数も負数も同じ表示となり,判別できない.
| 10進 | 2進正数 | 10進 | 2進負数 | ||||||||
| 正数 | 負数 | ||||||||||
| |
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| +1 | 0 | 0 | 0 | 0 | 1 | -1 | 1 | 1 | 1 | 1 | 1 |
| +2 | 0 | 0 | 0 | 1 | 0 | -2 | 1 | 1 | 1 | 1 | 0 |
| +3 | 0 | 0 | 0 | 1 | 1 | -3 | 1 | 1 | 1 | 0 | 1 |
| +4 | 0 | 0 | 1 | 0 | 0 | -4 | 1 | 1 | 1 | 0 | 0 |
| +5 | 0 | 0 | 1 | 0 | 1 | -5 | 1 | 1 | 0 | 1 | 1 |
| +6 | 0 | 0 | 1 | 1 | 0 | -6 | 1 | 1 | 0 | 1 | 0 |
| +7 | 0 | 0 | 1 | 1 | 1 | -7 | 1 | 1 | 0 | 0 | 1 |
| +8 | 0 | 1 | 0 | 0 | 0 | -8 | 1 | 1 | 0 | 0 | 0 |
| +9 | 0 | 1 | 0 | 0 | 1 | -9 | 1 | 0 | 1 | 1 | 1 |
| +10 | 0 | 1 | 0 | 1 | 0 | -10 | 1 | 0 | 1 | 1 | 0 |
| +11 | 0 | 1 | 0 | 1 | 1 | -11 | 1 | 0 | 1 | 0 | 1 |
| +12 | 0 | 1 | 1 | 0 | 0 | -12 | 1 | 0 | 1 | 0 | 0 |
| +13 | 0 | 1 | 1 | 0 | 1 | -13 | 1 | 0 | 0 | 1 | 1 |
| +14 | 0 | 1 | 1 | 1 | 0 | -14 | 1 | 0 | 0 | 1 | 0 |
| +15 | 0 | 1 | 1 | 1 | 1 | -15 | 1 | 0 | 0 | 0 | 1 |
| +16 | 1 | 0 | 0 | 0 | 0 | -16 | 1 | 0 | 0 | 0 | 0 |
減算の実習
![]() 結線およびスイッチの設定
結線およびスイッチの設定
- 電源スイッチをOFFにする.
- 端子1と2,4と18,7と17,10と11,15と16および21と22をリードチップで接続する. (図19参照)
- 「A」累算器のシフト方向スイッチを,,
 印方向に設定する.
印方向に設定する.
- 「B」
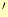 レジスタの表示器ON/OFFスイッチを,ONにする.
レジスタの表示器ON/OFFスイッチを,ONにする.
- 「M」レジスタの表示器ON/OFFスイッチを,OFFにする.
- 10進数表示器ON/OFFスイッチを,左右の2個ともOFFにする.
- 「A」
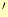 /「A」切換スイッチをいったん「A」側に設定する.
これは,演算結果によりどちらかを選ぶためである.演算結果が正数のときは
「A」側に,負数のときは「A」
/「A」切換スイッチをいったん「A」側に設定する.
これは,演算結果によりどちらかを選ぶためである.演算結果が正数のときは
「A」側に,負数のときは「A」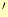 側に設定する.
側に設定する.
- 電源スイッチをONにし,以下の操作をおこなう.
![]() 操作順序
操作順序
具体的な数値(たとえば1-9=-8)を用いて,操作順序を説明する.演算の過程は,図 20 を使って,説明する. []
- =1pt =0.2pt CLをプッシュして,各レジスタの内容と表示をゼロにする.
- レジスタ選択(A)をプッシュする.
- 数字設定キーの=1pt =0.2pt 1をプッシュする.「A」累算器には,被減数1に 相当する2進数がセットされる.
- レジスタ選択スイッチの(B)をプッシュする.
- 数字設定キーの=1pt =0.2pt 9をプッシュする.「B」レジスタには,減数9に相当
する2進数がセットされ,「B」
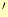 レジスタには,減数(「B」
レジスタ)の補数(補数)がセットされる.
レジスタには,減数(「B」
レジスタ)の補数(補数)がセットされる.
- =1pt =0.2pt ADDをプッシュして,「A」累算器と「B」
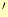 レジス
タの最下位ビット同士の加算をおこなう.S=0,C
レジス
タの最下位ビット同士の加算をおこなう.S=0,C
 =1とな
る.
=1とな
る.
- =1pt =0.2pt Iを1回プッシュして,「A」累算器と「B」
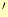 レジス
タの内容を,右へ1ビットシフトさせる.S=0のデータは「A」累算器
の最上位ビットに記憶され,C
レジス
タの内容を,右へ1ビットシフトさせる.S=0のデータは「A」累算器
の最上位ビットに記憶され,C
 =1のデータは桁上げメモリに記
憶されて,C
=1のデータは桁上げメモリに記
憶されて,C
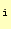 =1となる.(「B」レジスタの内容(減数)も,
ともにシフトするが,実際の演算には無関係となり,表示されているだけとな
る.)
=1となる.(「B」レジスタの内容(減数)も,
ともにシフトするが,実際の演算には無関係となり,表示されているだけとな
る.)
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=0,
C
 =1となる.
=1となる.
- Iを1回プッシュして,[7]と同様にシフトさせる.S=0のデータは
「A」累算器の最上位ビットに記憶され,C
 =1のデータは
桁上げメモリに記憶されて,C
=1のデータは
桁上げメモリに記憶されて,C
 =1となる.
=1となる.
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=1,
C
 =1となる.
=1となる.
- =1pt =0.2pt Iを1回プッシュして,[7]と同様にシフトさせる.S=1のデータは
「A」累算器の最上位ビットに記憶され,C
 =1のデータは
桁上げメモリに記憶されて,C
=1のデータは
桁上げメモリに記憶されて,C
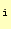 =1となる.
=1となる.
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=1,
C
 =1となる.
=1となる.
- =1pt =0.2pt Iを1回プッシュして,[7]と同様にシフトさせる.S=1のデータは
「A」累算器の最上位ビットに記憶され,C
 =0のデータは
桁上げメモリに記憶されて,C
=0のデータは
桁上げメモリに記憶されて,C
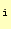 =0となる.
=0となる.
- =1pt =0.2pt ADDをプッシュして,[6]と同様に加算をおこなう.S=1,
C
 =0となる.
=0となる.
- =1pt =0.2pt Iを1回プッシュして,[7]と同様にシフトさせる.S=1のデータは
「A」累算器の最上位ビットに記憶され,C
 =0のデータは
桁上げメモリに記憶されて,C
=0のデータは
桁上げメモリに記憶されて,C
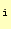 =0となる.以上の操作で,5ビッ
ト全部の演算が終了する.「A」累算器には,演算結果の差が記憶されて
いるが最上位ビットを見ると"1"なので,負数をあらわしている.
=0となる.以上の操作で,5ビッ
ト全部の演算が終了する.「A」累算器には,演算結果の差が記憶されて
いるが最上位ビットを見ると"1"なので,負数をあらわしている.
- 「A」累算器のデータが負数(最上位ビットが1)のときは,「A」
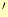 /「A」切換スイッチを「A」
/「A」切換スイッチを「A」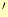 側に設定し,正数
(最上位ビットが0)のときは「A」側に設定する.
側に設定し,正数
(最上位ビットが0)のときは「A」側に設定する.
- 「A」累算器の2進数データを10進数表示するために,10進数表示器ON/OFFス イッチの左側のスイッチをONにすると,"12"と表示される.
![]() 注意
注意
- 累算をおこなう場合の負数判別は-1から-15までなので,あらかじめその範囲内 に入るように数値を設定すること.
- 累算をおこなう場合は,まずCP1をリセットする.その方法は,CP1の表 示が"0"になるように,=1pt =0.2pt Iをプッシュする.また,=1pt =0.2pt I IIをプッ シュすることによってもできる.なお,CLをプッシュすると,全部の設定 がリセットされるので注意が必要である.
- CP1をリセットしたのち,減数の実習の"操作順序"の[4]以降を,再度 操作すること.累算がおこなわれる.
- 減算の実習は,図18(累算器を用いた減算回路)を用 いるが,図17(減算の基本回路)の方式は,「M」 レジスタに補数器がないためにできない.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年10月21日
![\includegraphics[keepaspectratio, scale=1.0]{figure/logic2/MIL_half_adder_1.eps}](img25.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/logic2/MIL_half_adder_2.eps}](img26.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/MIL_full_adder_1.eps}](img27.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/MIL_full_adder_2.eps}](img28.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/exp_half_adder_1.eps}](img29.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/exp_half_adder_2.eps}](img30.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/exp_full_adder_1.eps}](img31.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/exp_full_adder_2.eps}](img32.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/MIL_encoder.eps}](img37.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/exp_encoder.eps}](img38.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/MIL_decoder.eps}](img49.png)
![\includegraphics[keepaspectratio,scale=0.8]{figure/logic2/exp_decoder.eps}](img50.png)
![\begin{table}
\begin{center}
\includegraphics[keepaspectratio, scale=1.0]
{figure/logic2/table_kasan_dousa.eps}
\end{center} \end{table}](img62.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/serial_add_method.eps}](img63.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/accum_add_method.eps}](img64.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/sequence_add.eps}](img70.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/serial_sub_method.eps}](img71.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/logic2/accum_sub_method.eps}](img72.png)
![\includegraphics[keepaspectratio,origin=c,angle=90,scale=0.85]{figure/logic2/exp_sub.eps}](img73.png)