2 プリプロセッサー(15章)
2.1 プリプロセッサの実行タイミング(p.282)
「gcc」を使って、ソースプログラムをマシン語に直すとき、通常はコンパイルす ると言うが、実際にはコンパイル以外の作業も行っている。教科書のp.282に示されてい るように、コンパイルの前にプリプロセッサーがソースファイルを書き直している。そして、 コンパイルの後、リンカーがいろいろなファイルを寄せ合わせて実行可能なファイルを作 成する。プリプロセッサーができることは、教科書のp.283の表に示されている。いろいろな機能 があるが、本講義で使うのは
- ファイルの挿入を行う#include
- マクロ定義を行う#define
2.2 プリプロセッサの使い方
プリプロセッサーの書式は、以下の通りです。今まで、さんざん書いてきているので、大 体理解はできると思います。#コマンド パラメーターリスト
このプリプロセッサーの書式には、以下の約束があります。
- #の前後に空白が有っても良い。#とコマンドの間に空白が有っても良いのですが、 プログラムがわかりにくくなりますので、通常は#とコマンドの間に空白は置きま せん。
- プリプロセッサーコマンドは、その行で終わりです。C言語の文のように';'が来る まで有効ということは有りません。したがって、文の区切りを表す';'もありませ ん。
- ただし、プリプロセッサーコマンドを複数行にわたって、記述したい場合、行の終 わりに'をつけて、次行と接続することができます。
2.2.1 ファイルの挿入
#include “ファイル名”は、指定されたテキストファイルとこの行を置き換えま す。ファイル名が<filename> で書かれた場合には、システムに定義されたファイルです。 unix では、/usr/include にあるファイルで置き換えられます。プログラマーが作 成したファイルを挿入したい場合は、 #include "myfile.h" のように記述します。 プログラマーが自分でヘッダーファイルを書くことがあります。例えば、大規模なプログ ラムを作成する場合、ファイルは1つではなく、いろいろな部分を別々のファイルに書い て、それをあとであわせて、1つのプログラムにすることがあります(分割コンパイル)。 その場合には、共有する構造体や大域変数を1つのファイルにして、myfile.h とい うファイルを作り、それぞれのファイルで#include することがよくあります。こ のようにすると、同じ文をそれぞれのファイルに記述する必要が無くなり、タイピングが 楽になるとともに、ミスが減ります。ここでの学習では、分割コンパイルをするほどのプログラムを書くことはないでしょう。 将来、比較的大きなプログラムを書くときに、勉強してください。 本来、次のサンプル のような使い方はしませんが、#includeの動作の理解のために、実行させてみてください。 #includeにより、そこの行が指定のファイルに置き換わっているのが理解できます。 実 行の結果、使い方によっては、便利そうであることが分かりましたか?。ただ、注意して 欲しいことは、この行の置き換えはコンパイルの前に行われることです。コンパイルによ り実行ファイルが出来上がった後に、ヘッダーファイルを書き換えても、それは反映され ません。言いたいことは、ここにデータを書いた場合、その変更を反映させるためには、 再度コンパイルが必要ですということです。
Hello World !!を出力するおなじみのプログラムです。プログラムの一部が、
myfile.hにかかれています。以下が、C言語のソースプログラムです。変なプログラ
ムですが、ヘッダーファイルがちゃんと書かれていれば、実行可能です。
![\begin{lstlisting}[caption=マクロを使ったプログラム,label=prog:macro]
...](img1.png)
これをコンパイルして、実行ファイルを作るためには、以下のヘッダーファイル
(myfile.h)も必要です。当然、ファイル名はソースプログラムの指定通りにする必
要があります。いかがヘッダーファイルです。
![\begin{lstlisting}[caption=ヘッダーの例,label=prog:my_head]
int main(){
printf(''Hello World !!\n'');
\end{lstlisting}](img2.png)
2.2.2 マクロ定義
#includeはその行を指定のファイルで置き換えましたが、#defineはファイル 内の文字列を指定の通りに置き換えます。単純な文字列の置き換えと、引数を含む文字列 の置き換えがあります。この引数を含む文字列の置き換えをマクロ定義と言います。それ ぞれについて、説明します。
文字列置換
これは、以下のように記述します。
#コマンド パラメーターリストこのプリプロセッサーコマンドがあると、この行以降の'文字列1'が'文字列2'に、
#undef 文字列1があるまで、置き換わります。もし、#undefが無いと、そのファイルの最後の行までコマ ンドは有効になります。通常、文字列1はすべて大文字で記述します。別に小文字でも良 いのですが、ほとんどのプログラマーは大文字を使います。その方が、プログラムがわか りやすくなります。
引数付き置換
先に説明した単純な文字列の置き換えと似ています。ただ、関数のように引数が使えます。
記述は、以下の通りです。
#define マクロ名(引数) 引数を含む文字列
このプリプロセッサーコマンドも、
#undef マクロ名(引数)があるまで、有効です。もし、#undefが無いと、そのファイルの最後の行までコマンドは 有効になります。
2.3 プリプロセッサを使ったプログラム例
2.3.1 微分方程式
#defineを使ったサンプルとして、2階の常微分方程式の解を数値計算で求めます。2階の 常微分方程式の一般形は、です。いきなり、この微分方程式の解を求めるとなると、難しそうですが、いたって簡単 です。次ページに、プログラムを載せてあります。このプログラムのなかで、微分方程式 を計算しているのは、たった1行です。プログラムの後半にある
y[i]=2*y[i-1]+DY2DX2(x-dx,y[i-1])*dx*dx - y[i-2];だけです。たったこの1行で、皆さんが苦労した微分方程式が計算できます。
簡単なだけではなく、どんな形の微分方程式でも解けます。皆さんが数学の授業で苦労し た微分方程式は、解析解(解が初等関数の組み合わせ)があるものばかりです。この方法を 使うと、解析解が無いものまで計算可能です。驚いたでしょう。このようなことから、コ ンピューターによる数値計算では、実に有益な情報が得られることが理解できるでしょう。
それでは、重要なこの1行の内容を示します。やっと数値計算の授業らしくなってきまし た。まず、微分方程式を数値計算で解く場合、テイラー展開が重要になります。テイラー展開は、
です。これは、
となります。次に、(2)と(3)式の各辺どおし を足し合わせます。すると、
| (4) |
となります。この式の4次以上の項を無視して、ちょっとだけ変形すると、
| (5) |
となります。
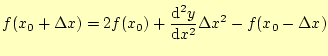 |
(6) |
となります。この式の右辺第2項は、与えられた微分方程式から、計算できます。式 (1)を代入すると
となります。
この式の右辺は、![]() と
と
![]() と
と
![]() の値がわかれば、
の値がわかれば、
![]() の値が計算できることを示しています。関数
の値が計算できることを示しています。関数![]() は問題により与えれ
ています。残りは、通常初期条件として、与えられます。すると、
は問題により与えれ
ています。残りは、通常初期条件として、与えられます。すると、
![]() が計算できま
す。この値をまた、式(7)に代入して、今度は、
が計算できま
す。この値をまた、式(7)に代入して、今度は、
![]() を計算します。これを順次繰り
返せば、いくらでも計算できます。この?xごとの計算結果が、まさに2階の常微分方程式
(1)の解になっています。
を計算します。これを順次繰り
返せば、いくらでも計算できます。この?xごとの計算結果が、まさに2階の常微分方程式
(1)の解になっています。
リスト3に示すプログラムでは、
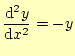 |
(8) |
を計算している。初期条件は、
| (9) | ||
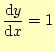 |
(10) |
です。この初期条件から、y(?x)を計算する必要があります。そのために、テーラー展開を使います。以下の通りです。
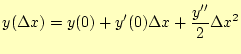 |
(11) |
これで、
実は、常微分方程式を数値計算により解く、もっと強力な方法があります。4次のルンゲ・ クッタの方法です。初期条件もこちらのほうが、簡単に表現できます。ただし、2階の微 分方程式を解くときには、ほんのちょっとだけ、工夫が必要です。今の段階で、それを説 明するのは、早すぎます。ルンゲ・クッタの方法を学習するときに説明します。
2.3.2 プログラム例
- 1行
- 解くべき微分方程式、
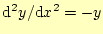 を引数付き置換で定義している。
を引数付き置換で定義している。
- 2行
- 微分方程式の初期条件、
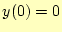 を引数付き置換で定義している。
を引数付き置換で定義している。
- 3行
- 微分方程式の初期条件、
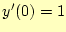 を引数付き置換で定義している。
を引数付き置換で定義している。
- 4行
- 計算ステップ数を文字型置換で設定している。プログラム中のNが全て1000 に置き換わる。
- 5行
- 計算の上限を文字型置換で設定している。プログラム中のMAX_Nが全て、 10.0に置き換わる。
- 20-21行
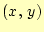 の値をファイルに書き込んでいる。
の値をファイルに書き込んでいる。
- 28行
- 微分方程式を計算している。
- 29行
- 計算結果
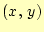 の値をファイルに書き込んでいる。
の値をファイルに書き込んでいる。
![\begin{lstlisting}[caption=微分方程式を計算するプログラム,label=prog:diff_eq]
...](img36.png)
2.3.3 実行と表示
作成したプログラムを実行すると、計算結果のファイル(cal_result)が作成されま す。これは、各行に- ターミナルからgnuplotを起動させます。コマンドは、「gnuplot」です。
[yamamoto]$ gnuplot
- gnuplotが起動したら、計算結果の描画です。コマンドは、plot "ファイル名"で
す。コマンドを送ると、図1のようなグラフが書かれ
るはずです。
gnuplot> plot "cal_result" - gnuplotを終了するときにコマンドは、exitです。
gnuplot> exit
- [練習1]
- リスト3のプログラムを実行せよ。
- [練習2]
- リスト3と式の関係を調べよ。
- [練習3]
- リスト3を書き換えて、他の微分方程式を 解いて見よ。
- [練習4]
- 計算ステップ数と誤差の関係を調べよ。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年6月6日



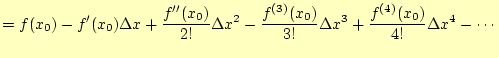
![\includegraphics[keepaspectratio, scale=0.7]{figure/sin.eps}](img38.png)