2 数値計算の基礎

[問 1]

テイラー展開の公式を導き出せ。公式を書くだけではだめである。3〜 4年生の数学の教科書に書かれているはずである。

[問 2]

問1の結果を利用して、関数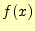$f(x)$を$x=a$の周りでテイラー展開する 式を示せ。

[問 3]

問1の結果を利用して、関数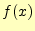$f(x)$を$x=0$の周りでテイラー展開す る式を示せ。これをマクローリン展開と言う。

[問 4]

問1の結果を利用して、関数 $f(x+\Delta x)$を$x$の周りでテイラー展 開する式を示せ。

[問 5]

次の3つの関数を、$x=0$の周りでテイラー展開、即ちマクローリン 展開せよ。以下の3つの関係は、どうなっているか考察せよ。

$$e^{x}=$$

$$\sin x=$$

$$\cos x=$$

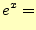
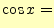
[問 6]

以下の連立方程式を行列とベクトルで表現せよ。

$$a_{11}x_1+a_{12}x_2+a_{13}x_3+\cdots+a_{1N}x_N =b_1$$

$$a_{21}x_1+a_{22}x_2+a_{23}x_3+\cdots+a_{2N}x_N =b_2$$

$$a_{31}x_1+a_{32}x_2+a_{33}x_3+\cdots+a_{3N}x_N =b_3$$

$$\vdots\hspace{30mm}$$

$$a_{M1}x_1+a_{M2}x_2+a_{M3}x_3+\cdots+a_{MN}x_N =b_M$$

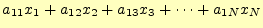
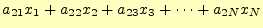
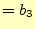
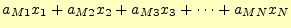
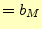
[問 7]

以下の連立方程式を行列とベクトルで表現せよ。

$$x_1+2x_2 -x_3+3x_4 =1$$

$$-2x_1-3x_2 -5x_4 =2$$

$$2x_1+2x_2+3x_3+5x_4 =3$$

$$-x_1+3x_2-12x_3 =4$$

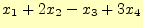
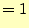
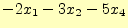
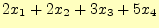
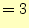
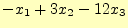
[問 8]

前問の連立方程式の解と係数行列の逆行列を求めよ。解と逆行列は 掃き出し法を使うこと。

ホームページ: Yamamoto's laboratory
著者: 山本昌志