4 円周率の計算
夏休み明けに円周率10万桁計算のプログラミングコンテストを行う。これは、必須ではな いが、興味のある者はプログラムを作成せよ。この部分は、山形大学の新関久一さんの 「プログラミング演習 III」を参考にさせてもらっている。最初に、ヒントとして、長桁計算のプログラムを示す。4.0.1 長桁計算
円周率を10万桁まで求めようとすると、長桁の計算が必要になる。しかし、C言語の倍精 度実数は20桁程度しか有効数字がない。そこで、長桁計算を考えることにする。人間は時間と紙さえあれば、いくらでも長い桁の計算ができる。ただの計算なので、人間ができてコン ピューターができないわけがない。人間と同じことをコンピューターにやらせれば良いの である。人間と同じように、コンピューターに長桁の筆算の計算をさせる。紙の代わりに データは配列に記憶させるだけである。
これを最初から考えるのは、初心者には少し難しいので、リスト2に プログラムを載せておく。このプログラムでは、非常に大きな桁数の2つの整数を入力し て、その和と差を計算することができる。
このプログラムでは、負の値は10の補数を用いている。もしある数が負の整数であれば、
その絶対値の各桁を10から差し引いて、最後に1を加えている。この辺のところは、3年生
の電子計算機の授業で教えたはずである。ただ、そのときは2進法を使っていたので、2の
補数だったが、考え方は同じである。
1 #include <stdio.h>
2 #include <string.h>
3 #include <stdlib.h>
4 #define N 32768
5 #define RADIX 10
6
7 void lf_scan(int n[]);
8 void lf_plus();
9 void lf_minus();
10 void lf_print(int n[]);
11 void lf_complement(int n[]);
12 void prt_bit(int n[]);
13 int a[N], b[N], Acc[N];
14
15 /*================================================================*/
16 /* main */
17 /*================================================================*/
18 int main(void){
19
20 lf_scan(a);
21 lf_scan(b);
22 lf_plus();
23 lf_print(Acc);
24 lf_minus();
25 lf_print(Acc);
26
27 return 0;
28 }
29
30
31 /*================================================================*/
32 /* lf_scan */
33 /*================================================================*/
34 void lf_scan(int n[]){
35 unsigned char key_in[N];
36 int i,l,flag=0;
37
38 scanf("%s",key_in);
39
40 l=strlen(key_in);
41
42 if(key_in[0] == '-'){
43 flag=1;
44 for(i=1; i<l; i++){
45 key_in[i-1]=key_in[i];
46 }
47 l--;
48 }
49
50 for(i=0;i<l;i++){
51 n[i]=(unsigned int)key_in[l-1-i]-48;
52 }
53
54 if(flag==1)lf_complement(n);
55 }
56
57 /*================================================================*/
58 /* lf_plus */
59 /*================================================================*/
60 void lf_plus(){
61 int i;
62
63 for(i=0;i<N;i++) Acc[i] = a[i]+b[i];
64
65 for(i=0; i<N-1; i++){
66 if(Acc[i] > 9)Acc[i+1]++;
67 Acc[i]%=RADIX;
68 }
69
70 Acc[N-1]%=RADIX;
71
72 }
73
74 /*================================================================*/
75 /* lf_minus */
76 /*================================================================*/
77 void lf_minus(){
78
79 lf_complement(b);
80 lf_plus();
81
82 }
83
84 /*================================================================*/
85 /* lf_print */
86 /*================================================================*/
87 void lf_print(int n[]){
88 int i,j,flag=0;
89
90 i=N-1;
91
92 if(n[i]>4){
93 flag=1;
94 lf_complement(n);
95 printf("-");
96 }
97
98 while(n[i]==0 && i>0) i--;
99 for(j=i;j>=0;j--)printf("%d",n[j]);
100
101 if(flag==1)lf_complement(n);
102
103 printf("\n");
104
105
106 }
107
108 /*================================================================*/
109 /* complement */
110 /*================================================================*/
111 void lf_complement(int n[]){
112 int i;
113
114 for(i=0; i<N; i++) n[i]=9-n[i];
115
116 n[0]++;
117
118 i=0;
119 while(n[i]==10 && i < N){
120 n[i]=0;
121 n[i+1]++;
122 i++;
123 }
124 }
4.0.2 円周率の計算
足し算と引き算の長桁の計算方法は分かった。わり算も同じである。後は自分で考えて、 マチンの公式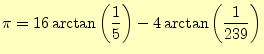 |
とテイラー展開
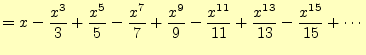 |
||
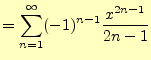 |
を用いて、10万桁を計算するプログラムを作成せよ。
4.1 課題提出要領
提出方法は、次の通りとする。
期限 8月25日(木) AM 8:55 用紙 A4 提出場所 山本研究室の入口のポスト 表紙 表紙を1枚つけて、以下の項目を分かりやすく記述すること。 授業科目名「計算機応用」 課題名「課題 夏休みの宿題」 5E 学籍番号 氏名 提出日 内容 ソースプログラム(プリントアウトでも、手書きでもOKとする)
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日