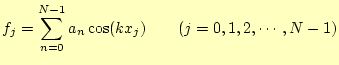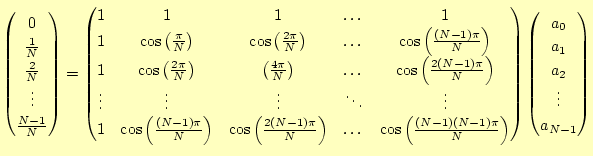2 計算機によるフーリエ級数

2.1 離散フーリエ変換(フーリエ$\cos$ 展開)

ここでは，計算機によりフーリエ変換を行う方法を説明します．フーリエ変換 と言っても，実際はフーリエ級数の係数を求めているだけです．今までは数学 だったので，関数$f(x)$ は連続的な値でした．しかし，実際の測定量，例えば 電圧など連続的に測定してそのデータが蓄えられるわけでは有りません．連続 ではなく離散的なデータとなります．これを上手に扱いフーリエ変換する方法 を考えましょう．とは言っても，上手にフーリエ変換するFFTまではたどり着 きませんが，そのさわりを説明します．

ここでも話を簡単にするために，周期を$2\pi$ とします．そして，原点を境に 対称な場合を考えます．これは，連立方程式の練習問題がそうなっていたから で，一般的な問題に拡張することは容易です．一般化についても，後に示す私 の講義ノートを参照してください．

その，周期の半分[$0, \pi$ ]中でN個の等間隔でデータが得られたとします． 当然，原点を境に対称という仮定がありますので，[$-\pi, 0$ ]の値も分かっ ていますが，ここでは使いません．データが等間隔に並ぶということは重要で す³．すなわち，

$$x_j =\frac{\pi}{N}j\qquad(j=0,1,2,\cdots,N-1)$$ (14)

の点でデータが得られたものとします．ここで得られデータを

$$f_j=f(x_j)$$ (15)

とします．

さて，準備ができたので，実際のフーリエ級数の式 (1) を評価してみます．測定量である$f_j$ と $x_j$ はそれぞれN個しかありません．従って，フーリエ係数の$c_n$ もN個しか 決めることはできません．関数は対称と仮定していますので，反対称を示す $b_n$ はゼロとなり，$a_n$ の $n=0,1,2,\cdots,N-1$ を求めることになります． この$a_n$ を積分の式(11)を使わないで，連立方程式から 計算しようというのです．

すなわち，

$$f(x)=\sum_{n=0}^{N-1}a_n \cos(nx)$$ (16)

を満たす$a_n$ を求めることになります．ここで残された問題は，測定量の $x_j$ と$f_j$ から$a_n$ を決めることになります．これは比較的簡単で，

$$f_j=\sum_{n=0}^{N-1}a_n \cos(kx_j)\qquad(j=0,1,2,\cdots,N-1)$$ (17)

の連立方程式を解けば良いことが分かります．この式の形が分かりにくい．そ れではもう少し分かり易く書いてみましょう．

$$\begin{pmatrix}f_0\\ f_1\\ f_2\\ \vdots\\ f_{N-1} \end{pmatrix} =... ...) \end{pmatrix} \begin{pmatrix}a_0\\ a_1\\ a_2\\ \vdots\\ a_{N-1} \end{pmatrix}$$ (18)

$f_j$ と$x_j$ は既知なので，この連立方程式を解いて$a_j$ を計算することは 可能です．その解がフーリエ係数$a_n$ となります．高速フーリエ変換(First Fourier Transform 略してFFT)は，この$a_n$ をある工夫されたアルゴリズム で高速に計算しているだけです．

「なるほど，連立方程式ならば計算機は得意なので，式 (18)を解けば話は終わり」と思ってはいけません．こ こでの学習はこれを実際に計算してみることですが，実際には高速に計算する ためにいろいろと工夫ができます．何しろ，$N=1000$ 位になるとこの式を計算 するのに膨大な時間がかかりますので，計算時間の短縮が必要になります．

この計算を高速で行うように工夫したアルゴリズムが，離散フーリエ変換 (DFT)であったり高速フーリエ変換(FFT)と呼ばれるものです．これは，データ が等間隔で並んでいるという性質を利用する方法です．もう少し詳しい説 明は，私の5M実験の講義ノートの「フーリエ変換とその周辺」を見てください． URLは以下の通りです．

http://www.ipc.akita-nct.ac.jp/ yamamoto/lecture/2003/5M_Exp/lecture_5M_Exp/fourier_transform.pdf

2.2 練習問題について

式が分かったので練習問題の内容について説明します．練習問題は，図 1に示すデータから，フーリエ級数を求めようとするもので す．周期は$2\pi$ で，原点を中心に対称としています．図からも分かるように 三角波をフーリエ$\cos$ 展開することになります．

この波形のフーリエ級数は，積分ではなく式(18)の連 立方程式を解くことにより求めることができます．図1を表 す式は，以下の通りです．

$$\begin{pmatrix}0 \frac{1}{N} \frac{2}{N} \vdots \frac{N-1... ...) \end{pmatrix} \begin{pmatrix}a_0 a_1 a_2 \vdots a_{N-1} \end{pmatrix}$$ (19)

この連立方程式を解いて，式(16)に代入すれば， 離散的な点を通る式を求めることができます．最終的には，後述の ページの図2のようになります．

図 1: 練習問題のデータ

ホームページ: Yamamoto's laboratory
著者: 山本昌志