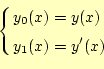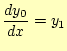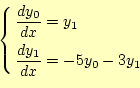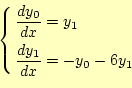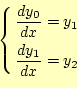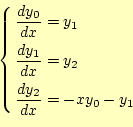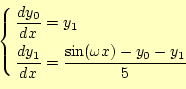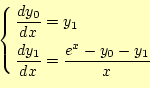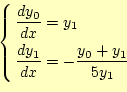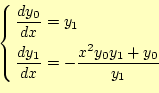Subsections

1 高階の常微分方程式

高階の常微分方程式を連立1階微分方程式に書き換えるという問題です。それにより高階の微分方程式でも、ルンゲ・クッタ法が使えるようになります。

1.1 問題(1)

$\displaystyle y^{\prime\prime}+3y^{\prime}+5y=0$

(1)

これは2階の常微分方程式ですから、2元1階常微分方程式に変形できるはずです。まず、

$\begin{equation*}\left\{ \begin{aligned} y_0(x)&=y(x)\ y_1(x)&=y^{\prime}(x) \end{aligned} \right.\end{equation*}$

と変数の変換をします。この変数変換により、

$\displaystyle \frac{dy_0}{dx}=y_1$

(3)

が直ちに導けます。これは求める2つの式の1つになります。

もう一つは、問題で与えられている式に変数変換の式(2) を適用します。すると、

	$\displaystyle y^{\prime\prime}+3y^{\prime}+5y=0$	(4)
	$\displaystyle \frac{dy_1}{dx}+3y_1+5y_0=0$	(5)
	(6)

となります。ここでは、

$\displaystyle \frac{dy_1}{dx}=y^{\prime\prime}$

(7)

を利用したことを忘れないでください。

したがって、式(3), (6)から、連立方程式は、

$\begin{equation*}\left\{ \begin{aligned} \frac{dy_0}{dx}&=y_1\ \frac{dy_1}{dx}&=-5y_0-3y_1 \end{aligned} \right.\end{equation*}$

となります。これが問題に対する解答です。

1.2 問題(2)

$\displaystyle y^{\prime\prime}+6y^{\prime}+y=0$

(9)

問題1と同じ方法で式を変形します。すると、

$\begin{equation*}\left\{ \begin{aligned} \frac{dy_0}{dx}&=y_1\\ \frac{dy_1}{dx}&=-y_0-6y_1 \end{aligned} \right.\end{equation*}$

を導くことができます。

1.3 問題(3)

$\displaystyle 5y^{\prime\prime}+2xy^{\prime}+3y=0$

(11)

これも問題(1)と同じです。ただ、式の中に

が入っているだけです。問題 (1)の式(2)と同じ変数変換すると、問題の式は、

$\displaystyle 5\frac{dy_1}{dx}+2xy_1+3y_0=0$

(12)

と変形できます。したがって、求める連立方程式は

$\begin{equation*}\left\{ \begin{aligned} \frac{dy_0}{dx}&=y_1\ \frac{dy_1}{dx}&=-\frac{1}{5}(3y_0+2xy_1) \end{aligned} \right.\end{equation*}$

となります。

1.4 問題(4)

$\displaystyle y^{\prime\prime\prime}+y^{\prime}+xy=0$

(14)

これは3階の常微分方程式ですが、考え方は2階の場合と全く同じです。変数の変換が

$\begin{equation*}\left\{ \begin{aligned} y_0(x)&=y(x)\ y_1(x)&=y^{\prime}(x)\ y_2(x)&=y^{\prime\prime}(x) \end{aligned} \right.\end{equation*}$

となるだけです。この変数変換によって、

$\begin{equation*}\left\{ \begin{aligned} \frac{dy_0}{dx}&=y_1\ \frac{dy_1}{dx}&=y_2 \end{aligned} \right.\end{equation*}$

を直ちに導くことができます。問題の式にこれらを代入すると

$\displaystyle \frac{dy_2}{dx}+y_1+xy_0=0$

(17)

となります。式(17), (18)から求める連立方程式は、

$\begin{equation*}\left\{ \begin{aligned} \frac{dy_0}{dx}&=y_1\ \frac{dy_1}{dx}&=y_2\ \frac{dy_2}{dx}&=-xy_0-y_1 \end{aligned} \right.\end{equation*}$

です。

1.5 問題(5)

$\displaystyle 5y^{\prime\prime}+y^{\prime}+y=\sin(\omega x)$

(19)

右辺に $\sin(\omega x)$ があり非同次微分方程式となっていますが、新しいことは何もありません。問(1)と同じように変数変換して、計算するだけです。解答は以下の通りです。

$\begin{equation*}\left\{ \begin{aligned} \frac{dy_0}{dx}&=y_1\ \frac{dy_1}{dx}&=\frac{\sin(\omega x)-y_0-y_1}{5} \end{aligned} \right.\end{equation*}$