1 1階の常微分方程式
1.1 4次のルンゲ・クッタ法
1.1.1 概要
前回の授業で学習した4次のルンゲ・クッタ法のプログラムの例をリスト 1に示す.このプログラムでは,微分方程式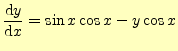 |
(1) |
を解く.このプログラムは,4つの関数から構成され,それぞれの役割は以下の通りであ る.
- main()関数
- 計算条件をキーボードより,読み込む
- 4次のルンゲ・クッタ法で微分方程式を計算する.
- 計算結果は,配列x[]とy[]に格納される.
- func()関数
- 導関数
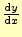 を計算する.
を計算する.
- 導関数
- mk_plot_data()関数
- gnuplotを用いて解をプロットするために,計算結果(x[],y[])をファ イルに書き出す.
- mk_graph関数
- gnuplotを呼び出して,解をプロットする.
1.1.2 使い方
このプログラムの使用方法は,以下の通りである.もし,異なった微分方程式を計算した ければ,func()関数を書き直せばよい.- 初期条件
 と
と を聞いてくるので,それぞれをキーボードから入力する.
を聞いてくるので,それぞれをキーボードから入力する.
- 計算終了の
 の値を聞いてくるので,それをキーボードから入力する.
の値を聞いてくるので,それをキーボードから入力する.
- 計算ステップ数を聞いてくるので,それをキーボードから入力する.
1 #include <stdio.h>
2 #include <math.h>
3 #define IMAX 100001
4 double func(double x, double y);
5 int mk_plot_data(char *a, double x[], double y[], int n);
6 int mk_graph(char *f);
7
8 /*================================================================*/
9 /* main function */
10 /*================================================================*/
11 int main(){
12 double x[IMAX], y[IMAX];
13 double final_x, h;
14 double k1, k2, k3, k4;
15 char temp;
16 int ncal, i;
17
18
19 /*--- set initial condition and cal range ---*/
20
21 printf("\ninitial value x0 = ");
22 scanf("%lf%c", &x[0], &temp);
23
24 printf("\ninitial value y0 = ");
25 scanf("%lf%c", &y[0], &temp);
26
27 printf("\nfinal x = ");
28 scanf("%lf%c", &final_x, &temp);
29
30 do{
31 printf("\nNumber of calculation steps( <= %d ) = ",IMAX-1);
32 scanf("%d%c", &ncal, &temp);
33 }while(ncal > IMAX-1);
34
35
36 /* --- size of calculation step --- */
37
38 h=(final_x-x[0])/ncal;
39
40
41 /* --- 4th Runge Kutta Calculation --- */
42
43 for(i=0; i < ncal; i++){
44 k1=h*func(x[i],y[i]);
45 k2=h*func(x[i]+h/2.0, y[i]+k1/2.0);
46 k3=h*func(x[i]+h/2.0, y[i]+k2/2.0);
47 k4=h*func(x[i]+h, y[i]+k3);
48
49 x[i+1]=x[i]+h;
50 y[i+1]=y[i]+1.0/6.0*(k1+2.0*k2+2.0*k3+k4);
51 }
52
53
54 /* --- make a graph --- */
55
56 mk_plot_data("out.txt", x, y, ncal);
57 mk_graph("out.txt");
58
59 return 0;
60 }
61
62
63 /*================================================================*/
64 /* define function */
65 /*================================================================*/
66 double func(double x, double y){
67 double dydx;
68
69 dydx=sin(x)*cos(x)-y*cos(x);
70
71 return(dydx);
72 }
73
74
75 /*==========================================================*/
76 /* make a data file */
77 /*==========================================================*/
78 int mk_plot_data(char *a, double x[], double y[], int n){
79 int i;
80 FILE *out;
81
82 out = fopen(a, "w");
83
84 for(i=0; i<=n; i++){
85 fprintf(out, "%e\t%e\n", x[i], y[i]);
86 }
87
88 fclose(out);
89
90 return 0;
91 }
92
93 /*==========================================================*/
94 /* make a graph */
95 /*==========================================================*/
96 int mk_graph(char *f){
97 FILE *gp;
98
99 gp = popen("gnuplot -persist","w");
100
101 fprintf(gp, "reset\n");
102 fprintf(gp, "set terminal postscript eps color\n");
103 fprintf(gp, "set output \"graph.eps\"\n");
104 fprintf(gp, "set grid\n");
105
106
107 /* ------- plat graph ---------*/
108
109 fprintf(gp, "plot \"%s\" using 1:2 with line\n",f);
110 fprintf(gp, "set terminal x11\n");
111 fprintf(gp, "replot\n");
112
113 pclose(gp);
114
115 return 0;
116 }
1.2 プログラムの説明
このプログラムの大まかな構成は,- main関数は,計算条件の設定と4次のルンゲ・クッタ法による計 算,グラフ作成のルーチンの呼び出しを行っている.
- 関数funcは,解くべき微分方程式
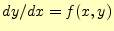 の
の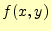 の
計算を行っている.
の
計算を行っている.
- 関数mk_plot_dataは,計算結果のxとyの配 列の値を,ファイル(ハードディスク)に保管している.
- 関数mk_graphは,ファイルからグラフを作成している.
各行の役割は,以下の通りである.
- 2行
- 数学関数を使っているので,math.hをインクルードしている.
- 3行
- 計算に使う配列の大きさIMAXを定義している.IMAXは最 大計算ステップ数に1以上を加えた値にしなくてはならない.
- 4-7行
- プログラマーが作成した関数のプロトタイプ宣言.
- 11行
- main関数の始まり.
- 12-16行
- main関数で使う変数や配列の宣言.
- 21-28行
- メッセージを書き出し,計算に必要な初期値と終値を取り込む.
- 30-33行
- 計算ステップ数の入力.ただし,配列の範囲を超えた場合,再度,入力を 促すようになっている.
- 38行
- 計算ステップのサイズ
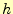 の計算.
の計算.
- 43-51行
- 4次のルンゲ・クッタ法の計算.
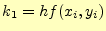
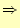
![$\displaystyle \texttt{k1=h*func(x[i],y[i])}$](img11.png)

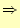
![$\displaystyle \texttt{k3=h*func(x[i]+h/2.0, y[i]+k2/2.0)}$](img14.png)
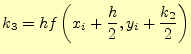
![$\displaystyle \texttt{k2=h*func(x[i]+h/2.0, y[i]+k2/2.0)}$](img17.png)
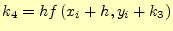
![$\displaystyle \texttt{k4=h*func(x[i]+h, y[i]+k3)}$](img20.png)
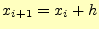
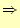
![$\displaystyle \texttt{x[i+1]=x[i]+h}$](img23.png)


![$\displaystyle \texttt{y[i+1]=y[i]+1.0/6.0*(k1+2.0*k2+2.0*k3+k4)}$](img26.png)
- 56行
- 計算結果をファイルに格納する関数(サブルーチン)の呼び出し.
- 57行
- ファイルに書かれたデータをgnuplotでグラフにする関数(サブルーチン)の 呼び出し.
- 59行
- main関数の戻り値.このプログラムでは,使われていない.
- 60行
- main関数の終わり.
- to 140mm
- 66行
- 関数funcの始まり.
- 関数名は,func
- 入力引数は,倍精度実数xと倍精度実数y
- 戻り値は,倍精度実数
- 67行
- 関数funcで使う変数宣言.
- 69行
- 解くべき微分方程式
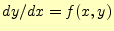 の
の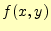 の計算.計算結果は,変数
dydxに格納.
の計算.計算結果は,変数
dydxに格納.
- 71
- 関数funcの戻り値を,変数dydxの値として与えている.
- 72
- 関数funcの終わり.
- to 140mm
- 78行
- 関数mk_plot_dataの始まり.
- 関数名は,mk_plot_data
- 入力引数は,文字列のポインターa,倍精度実数配列 xとy
- 戻り値は,整数
- 79-80行
- 関数mk_plot_dataで使う変数宣言.型名FILEは, ファイルを使うときに必要である.
- 82行
- ポインターaが示す文字列の名前で,書き込みモードでファイルを 開く.この後,ファイルは,outというポインターをつかってアク セスする.
- 84-86行
- ファイルへデータの書き込み.
- 88行
- ファイルを閉じる.
- 59行
- mk_plot_data関数の戻り値.このプログラムでは,使われていない.
- 60行
- mk_plot_data関数の終わり.
- to 140mm
- 96行
- 関数mk_graphの始まり.
- 関数名は,mk_graph
- 入力引数は,文字列のポインターa.これは,データファ イル名を表す.
- 戻り値は,整数
- 97行
- 関数mk_graphで使う変数宣言.型名FILEは, パイプを使うときに必要である.
- 99行
- 書き込みモードでファイルでパイプを開く.これは,ターミナルで, 「gnuplot -persist」と打ち込んだのと同じである.
- 101 -111行
- gnuplotにダブルクォーテションで囲んだ命令を与えている.
- 113行
- パイプを閉じている.
- 115行
- mk_graph関数の戻り値.このプログラムでは,使われていない.
- 116行
- mk_graph関数の終わり.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日