Subsections
1 プログラム方法
理論から分かるように,スプライン補間を行うためには以下の2つの計算が必要である.- 各点での2次導関数の値
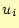 の計算
の計算
- 係数
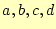 を求めて,補間の値の計算
を求めて,補間の値の計算
1.1 2次導関数の値を計算する関数
まず最初の関数で,標本点C言語の関数でこれを実現するための関数のプロトタイプ宣言は,
void spline_cal_u(int n, double x[], double y[], double u[]);のようにすればよい.nは標本点の最大の番号である.標本点の番号は,0から 始まりnで終わる.配列x[]とy[]に標本のxとy座標の値を入 れる.配列u[]は計算された2次導関数の値が入る.
この関数での処理の内容は,
- 標本点での2次導関数の値
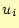 が満たす連立方程式を作成する.
が満たす連立方程式を作成する.
- その連立方程式を解く.
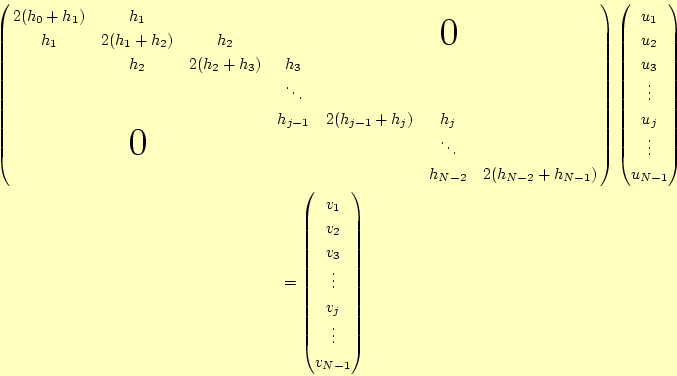 |
ただし,
| (2) | ||||
![$\displaystyle =6\left[\frac{y_{j+1}-y_j}{h_j} -\frac{y_j-y_{j-1}}{h_{j-1}}\right]$](img12.png) |
(3) |
この関数のフローチャートを図1に示す.この関数では, 連立方程式を解く必要がある.この連立方程式は,以下の特徴がある.
- 係数は,3重対角行列である.
- 対角成分は,ゼロにならない.
連立方程式により計算される2次導関数の値は,
![]() である.両端は自然境界条件で,
である.両端は自然境界条件で,
![]() とする.こ
この関数では最後にその条件を配列をu[0]=0, u[n]=0とすることで実
現している.
とする.こ
この関数では最後にその条件を配列をu[0]=0, u[n]=0とすることで実
現している.
1.2 補間の値を計算する関数
2次導関数の値が分かったので,残りの処理は,その値を利用して任意の
スプライン補間の計算に必要な
![]() から,補間点
から,補間点![]() の値を求める関数を作
ろう.C 言語の関数でこれを実現するための関数のプロトタイプ宣言は,
の値を求める関数を作
ろう.C 言語の関数でこれを実現するための関数のプロトタイプ宣言は,
double spline(int n, double x[], double y[], double u[], double xx);のようにすればよい.この関数の実引数xxに補関値を求めたい
この関数の処理の内容は,
- 補間値を求める
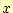 が,どの標本点の間にあるか探す.
が,どの標本点の間にあるか探す.
- 見つかった標本点の場所から,3次関数の係数を計算する.
- 3次関数から
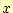 の時の値,
の時の値,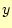 を計算する.
を計算する.
と計算できる.これらの係数から,補間の値
となる.
この関数のフローチャートを図2に示す.まず初めに,![]() が存在す
る区間を2分探索により探している.これがわかれば,
が存在す
る区間を2分探索により探している.これがわかれば,![]() を挟む場所の
を挟む場所の![]() の値がわ
かる.そうすると,式(4)〜(7)を用いて,3次関数の補間式
の係数
の値がわ
かる.そうすると,式(4)〜(7)を用いて,3次関数の補間式
の係数![]() の値が計算できる.そして,式(8)から補間値
の値が計算できる.そして,式(8)から補間値![]() がわかる.
補間したい点
がわかる.
補間したい点![]() が変わる毎にspline(n, x, y, u, xx)を呼び出せばよいわけで
ある.
が変わる毎にspline(n, x, y, u, xx)を呼び出せばよいわけで
ある.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2005-12-21
![\includegraphics[keepaspectratio,scale=0.7]{figure/spline_cal_u.eps}](img16.png)
![\includegraphics[keepaspectratio,scale=0.7]{figure/spline.eps}](img30.png)