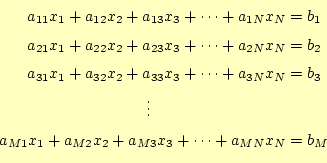Subsections
2 連立一次方程式
2.1 連立方程式の表現方法
連立1次方程式(Linear Equations)は、次のような形をしている。式(7)は行列とベクトルで書くと、式がすっきりして 考えやすくなる。書き直すと、
である。それぞれの行列とベクトルは、
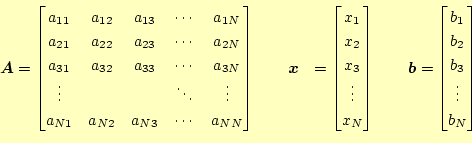 |
を表す。
通常、連立1次方程式(7)は
と書き表せる。このようにすると、見通しがかなり良くなる。
2.2 ガウス・ジョルダン法の基本的な考え方
ガウス・ジョルダン(Gauss-Jordan)法というのは、連立方程式 (10)を次にように変形させて、解く方法である。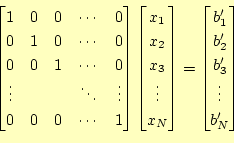 |
この式から明らかに、求める解
をガウス・ジョルダン法で解を求める。 解くべき、方程式
 |
2行
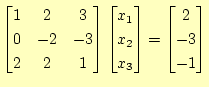 |
3行
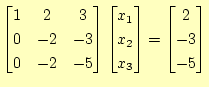 |
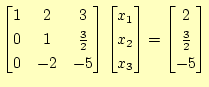 |
1行
 |
3行
 |
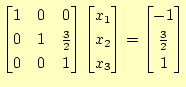 |
 |
これで、ガウス・ジョルダン法による対角化の作業は完了である。これか ら、
2.3 逆行列
ガウス・ジョルダンを使って,逆行列が求められる.以下のようにする.解くべき、方程式 |
とする.
2行![]() 1行
1行
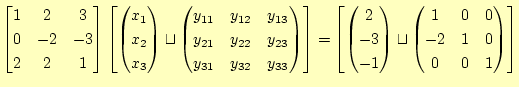 |
3行
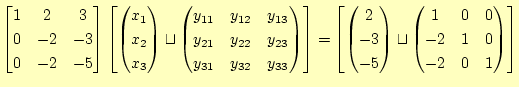 |
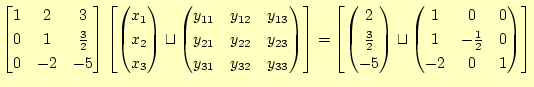 |
1行
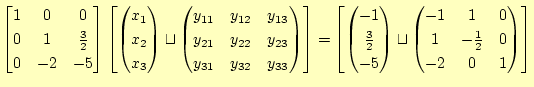 |
3行
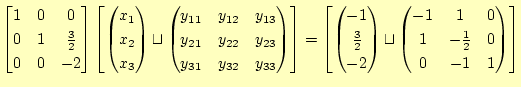 |
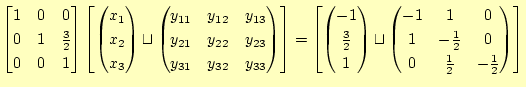 |
 |
これで、ガウス・ジョルダン法による対角化の作業は完了である。これか ら、
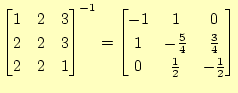 |
と分かる.
2.4 ガウス・ジョルダン法のC言語の関数
ピボット選択は行わないで、逆行列も求めないのガウス・ジョルダン法で連立方程式を計 算するプログラムを示す。このプログラムの動作は、次の通りである。- 仮引数「n」は、解くべき連立方程式の未知数の数である。
- 仮引数の配列「a」と「b」は、係数行列
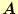 と非同次項
と非同次項
 である。
値は、呼び出し元からにアドレス渡しで送られる。
である。
値は、呼び出し元からにアドレス渡しで送られる。
- 係数行列は、配列「a[1][1]」〜「a[n][n]」に格納されている。
- 非同次項は、配列「b[1]」〜「b[n]」に格納されている。
- 連立方程式の解
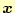 は、配列「b[1]」〜「b[n]」に格納される。
は、配列「b[1]」〜「b[n]」に格納される。
- このプログラムでの処理が終了すると、配列「a[1][1]」〜「a[n][n]」は単位 行列になる。。
/* ========== ガウスジョルダン法の関数 =================*/
void gauss_jordan(int n, double a[][100], double b[]){
int ipv, i, j;
double inv_pivot, temp;
for(ipv=1 ; ipv <= n ; ipv++){
/* ---- 対角成分=1(ピボット行の処理) ---- */
inv_pivot = 1.0/a[ipv][ipv];
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
/* ---- ピボット列=0(ピボット行以外の処理) ---- */
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
}
}
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2005-11-25