6 ファイル処理

実験データを整理したり、計算結果を他のプログラムで処理したりする場合、ファイル入出力の処理が必要不可欠である。ファイル処理の基本について学習する。

6.1 ファイルへデータ出力

先ほどの微分方程式(5.4.2)の数値計算の結果は、グラフに表示させた。ここでは、グラフに表示のみならず、解の値をファイルに出力する方法を示す。コンピュータープログラムでファイルを取り扱う場合、 OpenとCloseの処理が必要である。FORTRANやC言語でその処理が必要なように、 Mathematicaでも必要である。Mathematicaでは、次の手順でファイルへデータを書き出す。

OpenWriteコマンドで、ファイルをオープンする。
Writeコマンドで、データをファイルに書き込む。
Closeコマンドで、ファイルをクローズする。

先ほどの常微分方程式の結果を、ファイルに書き出すことを練習する。プログラムの動作は次のようにする。

計算すべき微分方程式は、式(5.4.2)の通りとする。
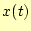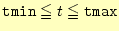微分方程式の解は、 $\texttt{tmin}\leqq t \leqq \texttt{tmax}$ の範囲計算する。
計算した範囲はプロットするとともに、num個の数値データとしてファイルに書き込む。

Mathematicaのプログラムは、次のようになる。このプログラムの大まかな動作を理解して、実行させてみよう。そして、書き込まれたファイルの中身を調べてみよう。このプログラムの各行の動作をプログラムの後に、説明している。

   tmin=0.0;
   tmax=10.0;
   num=1000;

   result=NDSolve[
      {x''[t]+ x'[t]+x[t]==0,x[0]==0,x'[0]==1},
      x,{t,tmin,tmax}
   ];

   f[t_]:=x[t]/.result[[1]];

   Plot[f[t],{t,tmin,tmax}];

   wfile=OpenWrite[
      "u:/temp/numerical_result.txt",
      FormatType->OutputForm
   ];

   For[i=0,i<=num, i=i+1,
      t=(tmax-tmin) i/num+tmin;
      Print[t,"\t",f[t]];
      Write[wfile,t,"\t",CForm[f[t]]];
   ];

   Close[wfile];

   Clear[tmin,tmax,num,t,i,f,x,result,wfile];

このプログラムの動作について、細かく説明しておく。

最初の3行で、変数tmin,tmin,numの値を設定している。
次のNDSolveコマンドで、微分方程式の解を数値計算している。微分方程式と初期条件、独立変数、解を計算する領域がそのコマンドの引数として与えられている。解は、Mathematicaの形式になっており、それを変数resultに代入している。
Mathematicaの形式である解は、x[t]/.result[[1]]で関数に直している。これについては、今はおまじないと思って欲しい ⁴。その解の関数は、 f[t_]:=とすることにより、関数f[t]と定義している。以降、解の値が必要なときは、関数f[t]を使う。
次のPlotコマンドにより、解をグラフ表示している。
次のOpenWriteコマンドにより、解の値を書き出すファイルをオープンしている。その第1引数がファイル名、第2引数はオプションで、ここでは出力形式をしている。このファイルは、wfileというストリーム⁵を使って、データを書き込むことができる。
次のFOR文でnum個の解のデータをファイルに書き出す。FOR文はループ制御で、初期値i=0、ループ条件i<=num、ループ後処理i=i+1で、それ以降の文を繰り返す。
データを書き出す時刻はtで、tminから tmaxまで、num個に分割している。
Print文で、データをディスプレイに書き出している。各行は、最初に時刻t、そして''\ t''によりタブ(Tab)を空け、関数f[t]の値を書き出している。時刻と関数の値の間にタブを入れるのは、データを書き出すときの常套手段である。
ファイルを使い終わったら、クローズしなくてはならない。Closeコマンドを使う。
もう一度、そのプログラムを実行させる場合、前回の変数が残っていると、思わぬ動作をすることがある。そのため、使った変数はクリアーするのが望ましい。Mathematicaでは、そのためのコマンド Clearが用意されている。

6.2 ファイルからデータ入力

次に、ファイルからのデータの入力方法について、説明する。これは、実験データなどをMathematicaで処理する場合、必要不可欠なテクニックなので、覚えておくと良い。

先ほど作成したデータをMathematicaで読み込み、処理をすることを考える。処理は、フーリエ変換を行うことにする。ここで、作成するプログラムの流れは、

ファイルからデータを読み込む。
読み込んだデータをプロットする。
データのうち、式(5.4.2)の解の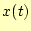の数値を抽出する。
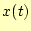の数値の列をフーリエ変換する。
フーリエ変換されたデータをプロットする。

である。実際の、プログラムは次のようになる。このプログラムの流れを理解して、実際に打ち込んで実行させよう。各行の説明は、プログラムリストの後に記述している。

   data=ReadList[
      "c:/temp/numerical_result.txt",
      {Number,Number}
   ];

   ListPlot[data];

   trdata=Transpose[data];
   xlist=trdata[[2]];

   ft=Fourier[xlist];

   ListPlot[
      Abs[ft],
      PlotRange->{{0,100},{0,5}},
      PlotJoined->True
   ];

このプログラムの動作について、細かく説明しておく。

ReadListコマンドで、データを読み込んでいる。第1引数でファイルを指定している。第2引数が、データの種類とその記述方法を示している。ここでは、各行に数値(Number)が2つ並んでいることを示している。読み込んだ結果は、リスト(行列みたいなもの)として、dataに格納される。
読み込まれたデータは、ListPlotコマンドでグラフ化されている。
Transposeコマンドで、行列dataの転置行列を trdataとしている。
trdata[[2]]で第2行、すなわち、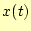のデータの数値列を抽出している。抽出された数値列は、xlistに格納される。
Fourierコマンドにより、xlistの数値列をフーリエ変換している。フーリエ変換されたデータは、ft変数に格納される。フーリエ変換された結果も数値列である。
ListPlotコマンドにより、フーリエ変換の結果をプロットしている。
- 第1引数が、プロットするデータである。一般に、フーリエ変換では複素数に変換されるので、絶対値化Absコマンドを用いて、実数に直している。
- PlotRangeオプションで、グラムの表示領域を指定している。横軸は0から100まで、縦軸は0から5までとしている。
- PlotJoinedオプションで、離散的なプロット点を直線で接続している。

ホームページ: Yamamoto's laboratory
著者: 山本昌志

Yamamoto Masashi
2005-11-28