3 フーリェ級数の例
フーリエ級数の係数を求める方法が分かった.本当に,任意の周期関数を三角関数の和に なっているかを,p.224の例題1と例題2を使って確かめる.3.1 矩形波
これまでの結果を利用して,図2のような矩形波をフーリエ級数で 表す.これは,教科書のp.224の例題1である.
![]() や
や![]() を求める積分の範囲は,
を求める積分の範囲は,
![]() である.しかし,図
2の関数は,
である.しかし,図
2の関数は,![]() で不連続になっている.そのため,
で不連続になっている.そのため,![]() と
と
![]() に分けて,積分を実施する.そうすると,
に分けて,積分を実施する.そうすると,
が得られる.積分は,教科書を見て自分でも計算すること.
この式の右辺は,本当に図2のような矩形波になっているのだろう
か?.コンピューターを使って計算してみる.ここで,フーリエ級数の部分和![]() を
を
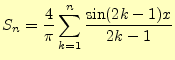 |
(16) |
とする.ちゃんとしたフーリエ級数であれば,
ここでの計算結果は,驚くべきことである.図2のような不連続な 関数は,式(15)のように三角関数を使って取り扱うことができる-- という事実6を 表している.このような不連続な関数は,電気回路ではしばしば現れる.デジタル回路の パルスは,矩形波である.今,諸君はパルスを解析する手段を得たことになる.電気回路 でおなじみの交流--サイン波-- の解析手法を用いて,パルスが解析できる!!!.
3.2 三角波
つぎに,図10のような三角波(教科書のp.224-225の例題2)をフーリエ 級数で表す.これも,が得られる. 式(17)の部分和を図11から16に 示す.矩形波より収束が早いことが分かるだろう.これまでの2つの結果から,フーリエ 級数は正しそうである--ということが感覚的理解できるであろう.本当は,自分でプロ グラムを書いてみることが重要であろう.プログラムの得意な者はトライせよ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年12月1日
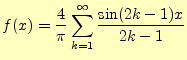
![\includegraphics[keepaspectratio, scale=1.0]{figure/rectangular.eps}](img128.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/rect_wave_1.eps}](img137.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/rect_wave_2.eps}](img140.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/rect_wave_3.eps}](img143.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/rect_wave_10.eps}](img146.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/rect_wave_100.eps}](img149.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/rect_wave_10000.eps}](img152.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/long_rect_wave.eps}](img155.png)
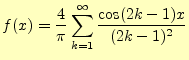
![\includegraphics[keepaspectratio, scale=1.0]{figure/triangle.eps}](img165.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/tri_wave_1.eps}](img168.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/tri_wave_2.eps}](img171.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/tri_wave_3.eps}](img174.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/tri_wave_10.eps}](img177.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/tri_wave_100.eps}](img180.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/tri_wave_10000.eps}](img183.png)