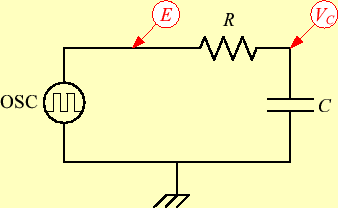
2 原理
図1のようなCR直列回路に交流電圧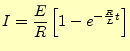 |
(1) | |
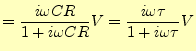 |
(2) |
となる.ここで,
 が抵抗,
が抵抗, は電源電圧の微分となる.また,コン
デンサーの電圧
は電源電圧の微分となる.また,コン
デンサーの電圧素子間の電圧を電源電圧との比[dB]であらわす,
| (3) | ||
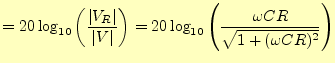 |
(4) |
となる.これを,周波数
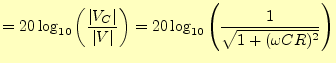 を横軸に,
を横軸に,同様に,電源との位相差は,
| (5) | ||
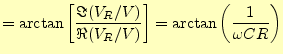 |
(6) |
となる.
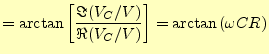 は実数部,
は実数部,
この図中の![]() は
は
![]() となる周波数で,これをCR回路の遮
断周波数と言う.このとき,位相差は,
となる周波数で,これをCR回路の遮
断周波数と言う.このとき,位相差は,
![]() [rad]=45 [deg]となる.
[rad]=45 [deg]となる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年7月3日
![\includegraphics[keepaspectratio, scale=1.0]{figure/CR_fresponce/graph.eps}](img145.png)