3 実験方法
3.1 周波数応答
3.1.1 微分回路
- 表1の機器を図3のよ うに接続する.
- 発振器の周波数を100[Hz]の正弦波にする.
- 発振器の出力電圧(実効値)が
 1[V]になるように,デジタルマルチメーターを見
ながら調整する.
1[V]になるように,デジタルマルチメーターを見
ながら調整する.
- オシロスコープのリサジュー図形を適当な大きさに調整し,図
5のx,Xあるいはy,Yをカーソル機能によって測定し,位相
角
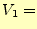 を次式
を次式
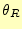
(7)
から求める. - 同時にデジタルマルチメーターの電圧
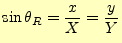 を記録する.そして,利得
を記録する.そして,利得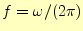 を
を
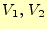 [dB]
[dB](8)
から算出する. - 以上の測定を次に周波数[HZ]について繰り返す.
200, 400, 600, 800, 1k, 1.5k, 2k, 3k, 4k, 5k, 6k, 7k, 8k, 9k,
10k, 20k, 40k, 60k, 80k, 100k, 200k
- 低い周波数領域での微分回路の実験では,リサジュー図形の
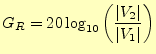 と
と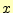 ,あるいは
,あるいは
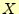 と
と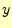 の区別がつかない(ほとんど同じ).そのため,2[kHz]以下の位相角の測
定は省く.
の区別がつかない(ほとんど同じ).そのため,2[kHz]以下の位相角の測
定は省く.
3.1.2 積分回路
- 表1の機器を図4のよ うに接続する.
- 発振器の周波数を100[Hz]の正弦波にする.
- 発振器の出力電圧(実効値)が
 1[V]になるように,デジタルマルチメーターを見
ながら調整する.
1[V]になるように,デジタルマルチメーターを見
ながら調整する.
- オシロスコープのリサジュー図形を適当な大きさに調整し,図
5のx,Xあるいはy,Yをカーソル機能によって測定し,位相
角
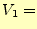 を次式
を次式
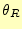
(9)
から求める. - 同時にデジタルマルチメーターの電圧
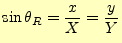 を記録する.そして,利得
を記録する.そして,利得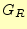 を
を
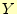 [dB]
[dB](10)
から算出する. - 以上の測定を次に周波数[HZ]について繰り返す.
500, 1k, 2k, 4k, 6k, 8k, 10k, 12k, 14k, 16k, 18k, 20k, 30k,
40k, 50k, 60k, 80k, 100k, 200k
- 高い周波数領域での積分回路の実験では,リサジュー図形の
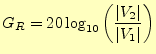 と
と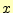 ,あるいは
,あるいは
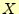 と
と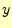 の区別がつかない(ほとんど同じ).そのため,80[kHz]以上の位相角の測
定は省く.
の区別がつかない(ほとんど同じ).そのため,80[kHz]以上の位相角の測
定は省く.
3.2 時間応答
3.2.1 微分回路
3.2.2 積分回路
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年7月3日
![\includegraphics[keepaspectratio, scale=1.0]{figure/CR_fresponce/diff_circuit.eps}](img156.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/CR_fresponce/int_circuit.eps}](img157.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/CR_fresponce/lissajous.eps}](img158.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/CR_fresponce/diff_rect.eps}](img159.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/CR_fresponce/int_rect.eps}](img160.png)