2 原理

2.1 ブール代数の公理

組み合わせ回路はブール代数で，表現することができる．それは，数学の理論で公理が決 められており，それを基礎として成り立っている．ブール代数は，

• 2項演算子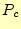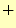$+$,$\cdot$と単項演算子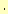$\bar{ }$が定義されてる．それ ぞれ加法と乗法，および補元の演算子を示す．
• 使われる変数は，0と1のみである．

の特徴をもっている．0と1だけからなる代数系であり，これはコンピューター内部で取り 扱うデータのビットと同じである．さらに，演算子もコンピューター内部の回路と一致し ている．そのようなことから，コンピューターに代表される論理回路の記述にブール代数 がよく使われる．

ブール代数の演算は，以下の公理で定義されている．

公理 2.1 (ブール代数)  

$$\hspace{3mm} A+B=B+A, \hspace{10mm} A \cdot B = B \cdot A$$ 交換法則 (1)

$$A \cdot(B + C)=(A \cdot B)+(A \cdot C), A+(B \cdot C) = (A+B) \cdot (A+C)$$ 分配法則 (2)

$$A+0=A, A \cdot 1 = A$$ 単位元 (3)

$$A + \bar{A}=1, A \cdot \bar{A}= 0$$ 補元 (4)

通常の数の演算と似ているが，異なる部分もある．それは，

• 式(2)の2つある分配法則のうちの一つが，数の計算の分配法 則に無い．
• 補元は逆元に似ていますが，異なる．

である．また，加法と乗法，補元の演算の結果は，必ず元の変数の集合$\{0,1\}$に含ま れる．このことをこれらの演算について閉じている¹と言う．

この公理から直ちにに分かる重要な性質がある．それは，加法の$+$と乗法の$\cdot$， 0と$1$をそれぞれ入れ替えても，同じ公理になる．このことから双対の原理

定理 2.1 (双対の原理)   ブール代数では，元の式の$+$と$\cdot$，0と$1$ を交換してできる式を元 の式の「双対」(dual)と呼ぶ．これは，ある定理が成り立つならば，その定理の 双対もまた成立する．

が成り立つ．

ブール代数においては加法と乗法は対等である．しかし，普通には，数の演算同様に乗法 は加法に先立って計算されるので注意が必要である．さらに，括弧を用いて，演算順序の 変更も可能としている．要するに，計算順序は普通の数の演算と同じと考えてよい．その ため乗法の記号$\cdot$が省略されたり，加法よりも乗法を演算順序を優先することを暗 黙の了解事項として書かれている場合が多い．このようなことは可能で問題は無いが，双 対の原理を考慮すると，加法と乗法の演算順序は対等とし，括弧で演算順序を決めて，さ らに乗法の記号もちゃんと書いた方が良いであろう．

2.2 ブール代数の諸定理

ブール代数の公理から導かれる重要な諸定理を示す．

定理 2.2 (演算の諸定理)  

$$\hspace{3mm} A+(B+C)=(A+B)+C, \hspace{20mm} A \cdot(B \cdot C) = (A \cdot B) \cdot C$$ 結合則 (5)

$$A+(A \cdot B)=A, A \cdot (A+B)=A$$ 吸収則 (6)

$$A+A=A, A \cdot A=A$$ 巾等律 (7)

$$A+1=1, A \cdot 0 = 0$$ (8)

$$A+(\bar{A}+B)=1, A \cdot (\bar{A} \cdot B)=0$$ (9)

$$(A+\bar{B}) \cdot (\bar{A}+B)=(A \cdot B)+(\bar{A} \cdot \bar{B}), (A \cdot \bar{B}) + (\bar{A} \cdot B)=(A + B) \cdot (\bar{A} + \bar{B})$$ (10)

$$\overline{(A+B)}=\bar{A} \cdot \bar{B}, \overline{(A \cdot B)}=\bar{A} + \bar{B}$$ ド・モルガン (11)

定理 2.3 (二重否定)  

$$\bar{\bar{A}}=A$$ (12)

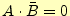定理 2.4   $A+\bar{B}=1$かつ $A \cdot \bar{B}=0$ならば，$A=B$である．

これらは，全て公理を用いて証明可能である．すなわち，公理からこれらの定理を導くこ とができる．

2.3 真理値表とMIL記号

ブール代数の変数の集合は$\{0,1\}$，演算子は$+$と$\cdot$， $\bar{ }$である．変数も演算子も少ないので，すべての組み合わせを表にすることは簡単 である．それを表1から3に示す．こ のように，変数の全ての組み合わせを示して，その演算結果を示すものを真理値表と言う． これら基本演算子の動作をする回路記号(MIL記号)も図1〜 3に示す．

これら基本演算に加えて，よく使われる論理回路の素子を図4〜 7に，その真理値表を表4〜に示す．

図 1: OR素子

図 2: AND素子

図 3: NOT素子

1. ORの真理値表

2. ANDの真理値表

3. NOTの真理値表

表 1: ORの真理値表

$A$	$B$	$A+B$
0	0	0
0	1	1
1	0	1
1	1	1

表 2: ANDの真理値表

$A$	$B$	$A \cdot B$
0	0	0
0	1	0
1	0	0
1	1	1

表 3: NOTの真理値表

$A$	$\bar{A}$
0	1
1	0

図 4: NOR素子

図 5: NAND素子

図 6: XOR素子

図 7: 一致素子

4. NORの真理値表

5. NANDの真理値表

6. XORの真理値表

7. 一致の真理値表

表 4: NORの真理値表

$A$	$B$	$\overline{A+B}$
0	0	1
0	1	0
1	0	0
1	1	0

表 5: NANDの真理値表

$A$	$B$	$\overline{A \cdot B}$
0	0	1
0	1	1
1	0	1
1	1	0

表 6: XORの真理値表

$A$	$B$	$A \oplus B$
0	0	0
0	1	1
1	0	1
1	1	0

表 7: 一致の真理値表

$A$	$B$	$A \odot B$
0	0	1
0	1	0
1	0	0
1	1	1

ホームページ: Yamamoto's laboratory
著者: 山本昌志