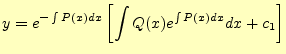2 二階線型常微分方程式
コイルとコンデンサーの両方が含まれる回路を表す微分方程式は,二階線型常微分方程式
になることが多い.「LCRの過渡応答」の実験では,
の形の微分方程式が現れる.ここで,
式(9)のように同次項がある時(非同次と言う),その一般解は,
の形で表すことができる.2階の非同次微分方程式を解く場合,これらの2つの階を求め, その和を一般解とするのは定石である.
式(9)の特殊解![]() は,簡単に分かる.それは,
は,簡単に分かる.それは,
| (10) |
となる.これを元の式に代入すれば,その解になっていることは直ちに分かる.
残る問題は,同次方程式
の一般解を探すことである.科学技術の分野では,このタイプの方程式では,
| (12) |
を解と仮定する.そして,これが解となるように
となる.すると,2次方程式の解の公式より,
| (14) |
とならなければならない.これら,2つの
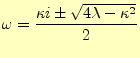 は,
は,
となる.これは,2階の微分方程式で2個の定数があり一般解にふさわしい.
ところが,式(13)が重根,すなわち,
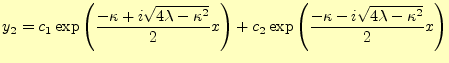 の場合,事情が異なる.式
(15)の未知数が一つなくなり,一般解とならない.
この場合,一般解
の場合,事情が異なる.式
(15)の未知数が一つなくなり,一般解とならない.
この場合,一般解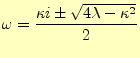 は
は
となる.元の式(11)に代入して確かめよ.
以上をまとめると,微分方程式(9)の一般解は,
| (17) |
となる.これは,
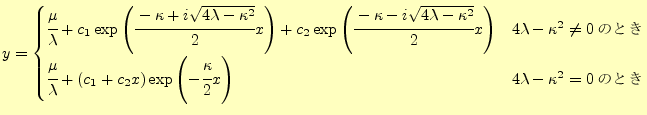 の値が正や負,0により,曲線の形がかなり
異なるので注意が必要である.
の値が正や負,0により,曲線の形がかなり
異なるので注意が必要である.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年7月3日