3 LCR直列回路
もっと実用的な常微分方程式を解くことにする.電気の諸問題の常微分方程式は2階の場
合が多い.例えば,図2のような回路である.最初,コンデ
ンサーにある電荷が蓄えられていたとする2.そうして,ある瞬間(t=0)にス
イッチSWをONにしたとする.この場合,回路に流れる電流は時間とともにどのように変化
するか? 数値計算によりそれを求めることにする.
まず,この回路に流れる電流の微分方程式を導かなくてはならない.これを,エネルギー
という観点から考えよう.コンデンサーとコイルに蓄えられたエネルギーの時間的な変化
が抵抗で消費される電力になる.コンデンサーに蓄えられるエネルギーは
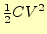 で,コイルに蓄えられるエネルギーは
で,コイルに蓄えられるエネルギーは
 である.一
方,抵抗で消費される電力は,
である.一
方,抵抗で消費される電力は,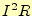 である.これらの関係を式で表すと,
である.これらの関係を式で表すと,
となる.
この式では,電流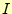 と電圧
と電圧 が時間の関数となっている.これでは見通しが悪いので,
電圧の項をコンデンサーの式を用いて消去することを考える.コンデンサーに蓄えられる
電荷を
が時間の関数となっている.これでは見通しが悪いので,
電圧の項をコンデンサーの式を用いて消去することを考える.コンデンサーに蓄えられる
電荷を とすると,
とすると,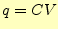 という関係がある.これから,
という関係がある.これから,
 が直ちに導かれる.ここで,電荷量の時間変化は電流と
なるので,
が直ちに導かれる.ここで,電荷量の時間変化は電流と
なるので,
 となることに注意する.これらの関係式を用いて,式
(5)を書き直す.すると,
となることに注意する.これらの関係式を用いて,式
(5)を書き直す.すると,
の関係式を導くことができる.最後の式の両辺の時間で微分すると,
となる.これで,電流 のみ常微分方程式になる.この最後の2階の微分方程式を解けば
よいわけである.
2階の常微分方程式を数値計算する場合,1階の連立常微分方程式に直すのがセオリーである.これは,
のみ常微分方程式になる.この最後の2階の微分方程式を解けば
よいわけである.
2階の常微分方程式を数値計算する場合,1階の連立常微分方程式に直すのがセオリーである.これは,
と変数変換を行う.すると,式(7)の最後の式は,
と書き直せる.これを配布したテキスト「常微分方程式の数値計算法」で示している高階
の微分方程式の数値計算法を使い4次のルンゲ・クッタ法で近似解を求める.
これを解くためには,LとC,Rの値と初期条件が必要である.それぞれを以下
のようにする.
- インダクタンス
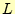 とキャパシタンス
とキャパシタンス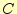 は,1とする.
は,1とする.
- スイッチSWをONにした瞬間(t=0),インダクタンス
 があるので電流は
流れない.
があるので電流は
流れない. となる.また,
となる.また,
 とする.
とする.
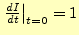 になるような電荷が蓄えられているわけであ
る.
になるような電荷が蓄えられているわけであ
る.
このような状況のもと,以下の場合について計算せよ.
- まずはじめに,
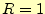 の場合について,電流の様子を計算せよ.
の場合について,電流の様子を計算せよ.
-
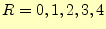 の場合について,電流の様子を計算せよ.臨界減衰の
時,どうなるか?
の場合について,電流の様子を計算せよ.臨界減衰の
時,どうなるか?
- 抵抗が電流に比例する場合
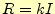 ,どうなるか計算せよ.
,どうなるか計算せよ.
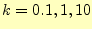 の場合
を計算してみよう.このような場合,非線形な方程式になる.従って,通常は解析
解ないが,数値計算は可能である.コンピューターは,すばらしい結果を与えてく
れる.
の場合
を計算してみよう.このような場合,非線形な方程式になる.従って,通常は解析
解ないが,数値計算は可能である.コンピューターは,すばらしい結果を与えてく
れる.
プログラムのヒントをあたえよう.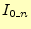 と
と は,それぞれ
I0[n]やI1[n]のような配列に格納する.そして,初期値は
I0[0]=0とI1[0]=1で表せる.ついでに時刻も配列
time[n]を使う.当然,time[0]=0で,
time[n+1]=time[n]+hのように計算する.最終的な解は,
I0[n]とtime[n]の関係が重要になる.
は,それぞれ
I0[n]やI1[n]のような配列に格納する.そして,初期値は
I0[0]=0とI1[0]=1で表せる.ついでに時刻も配列
time[n]を使う.当然,time[0]=0で,
time[n+1]=time[n]+hのように計算する.最終的な解は,
I0[n]とtime[n]の関係が重要になる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年10月18日
![]() で,コイルに蓄えられるエネルギーは
で,コイルに蓄えられるエネルギーは
![]() である.一
方,抵抗で消費される電力は,
である.一
方,抵抗で消費される電力は,![]() である.これらの関係を式で表すと,
である.これらの関係を式で表すと,
![]() と電圧
と電圧![]() が時間の関数となっている.これでは見通しが悪いので,
電圧の項をコンデンサーの式を用いて消去することを考える.コンデンサーに蓄えられる
電荷を
が時間の関数となっている.これでは見通しが悪いので,
電圧の項をコンデンサーの式を用いて消去することを考える.コンデンサーに蓄えられる
電荷を![]() とすると,
とすると,![]() という関係がある.これから,
という関係がある.これから,
![]() が直ちに導かれる.ここで,電荷量の時間変化は電流と
なるので,
が直ちに導かれる.ここで,電荷量の時間変化は電流と
なるので,
![]() となることに注意する.これらの関係式を用いて,式
(5)を書き直す.すると,
となることに注意する.これらの関係式を用いて,式
(5)を書き直す.すると,

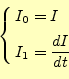
![]() と
と![]() は,それぞれ
I0[n]やI1[n]のような配列に格納する.そして,初期値は
I0[0]=0とI1[0]=1で表せる.ついでに時刻も配列
time[n]を使う.当然,time[0]=0で,
time[n+1]=time[n]+hのように計算する.最終的な解は,
I0[n]とtime[n]の関係が重要になる.
は,それぞれ
I0[n]やI1[n]のような配列に格納する.そして,初期値は
I0[0]=0とI1[0]=1で表せる.ついでに時刻も配列
time[n]を使う.当然,time[0]=0で,
time[n+1]=time[n]+hのように計算する.最終的な解は,
I0[n]とtime[n]の関係が重要になる.