2 数値計算法
2.1 オイラー法
常微分方程式を数値計算で解く方法の中でもっとも単純ではあるが,最も精度の悪い方法 である.よっぽどのことが無い限り,この方法で微分方程式を計算してはならない.ただ し,常微分方程式を数値計算することのイメージがつかみやすいので,学習する価値はあ る.もう一度,初期条件を含めて数値計算により解くべき方程式を示す.
 |
初期条件 | (6) |
この微分方程式の解を
となる.この式の右辺第2項は,式(6) から計算で きる.したがって,テイラー展開は,
| (8) |
と表すことができる.
オイラー法での数値計算では,計算の刻み幅![]() は十分に小さいとして,
は十分に小さいとして,
| (9) |
を計算する.式(5)と全く同じである.このとき計算の精度は1次と 言う3.
オイラー法をまとめると,以下に示すように微分方程式は差分方程式に近似できる.
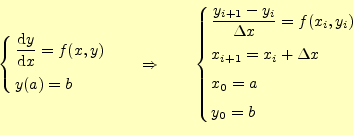 |
これれから,オイラー法での数値計算の漸化式
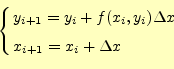 |
となる.初期値
実際にプログラムを行うときは,forやwhileを用いて繰り返し計算を行う(芋
づる式の部分).そして,計算結果の![]() と
と![]() は,配列x[i] やy[i]に格納
する.
は,配列x[i] やy[i]に格納
する.
x[0]=a;
y[0]=b;
dx = きざみ幅の計算
for(計算終了条件){
x[i+1]=x[i]+dx;
y[i+1]=y[i]+f(x[i],y[i])*dx;
}
この方法の計算のイメージは,図4の通りである.明らかに,出発 点の導関数のみ利用しているために精度が悪い.式も対称でないため,逆から計算すると 元に戻らない.
2.2 2次のルンゲクッタ法
2次のルンゲ・クッタと呼ばれる方法は,いろいろある.ここでは,代表的なホイン法と 中点法を示す.オイラー法は1次の精度であったが,これらは2次の精度になる.2.2.1 ホイン法
2.2.1.1 漸化式
先に示したように,オイラー法の精度は1次です.それに対して,2次のルンゲ・クッタ法 の精度は2次となる.今まで刻み幅を2次の精度ということは,テイラー展開より
| (12) |
となっていることを意味する.即ち,計算アルゴリズムが,
となっている必要がある.
式(13)から分かるように,![]() の増分
の増分![]() を計算するためには,
1階微分と2階微分の2項を満たす式が必要である.そうすると少なくとも,2点の値が必要と
なる.2点として,計算区間の両端の導関数の値を使うことにする.この導関数は問題とし
て与えられているので,計算は簡単である.そうして,区間の増分を
を計算するためには,
1階微分と2階微分の2項を満たす式が必要である.そうすると少なくとも,2点の値が必要と
なる.2点として,計算区間の両端の導関数の値を使うことにする.この導関数は問題とし
て与えられているので,計算は簡単である.そうして,区間の増分を
![]() のパ
ラメーターとした和で表現する.即ち,
のパ
ラメーターとした和で表現する.即ち,
とあらわすのである.この
![[*]](crossref.png) )と同一にできる.
)と同一にできる.
この式を![]() の周りでテイラー展開すると
の周りでテイラー展開すると
| (15) |
となる.これを,式(13)と比べると,
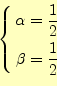 |
が得られる.これで,必要な式は求まった.まとめると,式 (6)を数値計算で近似解を求めるには
を使うことになる.何のことはない,出発点と終着点の平均の傾きを使っているのである. この式のイメージは,図5の示すところである.オイラー法では,区間の 平均の傾きを出発点だけで決めていたが,ホイン法は両端で決めているのである.これに より,計算精度が向上するのである.
2.2.1.2 精度の検証
よく見ると,この式(17)は,本当に2次の精度なのか?,と疑問が湧く.まずは,少なくとも2次の精度があることを確認である.漸化式は,
と変形できる.この結果は,まさに式(7)と同じ形をしており,少なくとも 2次の精度があることが確認できる.
次に3次の精度がないことを示す.テイラー展開の3次の項は,係数は無視すると,
となる4.
一方,ホイン法の3次の精度を表すのは,式(18)の右辺のテ イラー展開の2次の項である.これは,
となる.
明らかに,テイラー展開の3次の項である式(19)とホイ ン法の3次の項の式(20)は異なっている.したがって,ホイ ン法は3次の精度がないことが分かる.少なくとも2次の精度があって,3次の精度がない ことが示されわけで,ホイン法は2次の精度であることが証明されたことになる.
2.2.2 中点法
2.2.2.1 漸化式
これも,ホイン法と同じ2次の精度である.ホイン法は区間の両端の点の導関数 を使ったが,中点法は出発点と中点で漸化式を作る.先ほど同様,2点を使うので,2次の精度 にすることができる.ホイン法の式(14)に対応するものは,である.これを
 |
(22) |
となる.これを,式(13)と比較すると,
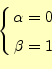 |
となる必要がある.したがって,中点法の漸化式は,
となる.この公式のイメージを,図6に示しておく.
2.2.2.2 精度の検証
式(18)と同じ手順でを用いることにより,中点法が2次の精 度であることが証明できる.漸化式をテーラー展開すると,が導かれる.ホイン法の場合と同様,これは,式(7)の2次の部分まで等 しいので,少なくとも2次の精度があることが分かる.一方,3次の精度がない ことは,以下の通り明らかである.式(20)と比べ て,微小変位
と直ちに導くことができる.これは,式(19)と異なりま すので,3次の精度がないことがはっきりしている.
2.3 4次のルンゲ・クッタ法
今まで示したオイラー法や2次のルンゲ・クッタ法のように,パラメーターを増やして誤 差項の次数を上げていく方法で,最良の方法と言われるのが4次のルンゲ・クッタ法であ る.パラメーターを増やして,5, 6, 7,
ということで,皆さんが常微分方程式を計算する必要が生じたときは,何はともあれ4次
のルンゲ・クッタで計算すべきである.「この問題を解く場合,4次のルンゲクッタだな」
と一言いってプログラムを書き始めると,おぬしできるな--と思われること間違いなし
である.間違っても「2次のルンゲ・クッタ![]() 」と言ってはならない.「4次の方
が
」と言ってはならない.「4次の方
が![]() 」と言う輩が必ずでてくる.普通の科学に携わる者にとって,4次のルンゲ・
クッタは常微分方程式の最初で最後の解法である.
」と言う輩が必ずでてくる.普通の科学に携わる者にとって,4次のルンゲ・
クッタは常微分方程式の最初で最後の解法である.
ただし,4次のルンゲ・クッタ法よりも精度の良い方法があることも知っておく必要があ る.より高精度な方法として,Bulirsch-Store法や予測子・修正法などがある.進んだ勉強を したいときに,学習するのがよいだろう.例えば文献 [1]等に詳しくかかれてい る.
4次のルンゲ・クッタの公式は,式(27)に示す通りである.そして,これ のイメージは図7のように表すことができる.
2次の場合と同じ手順で,公式を導き,そして4次の精度であることが証明できるであろう. しかし,計算は明らかに大変なので,腕力のある人はトライせよ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年8月8日
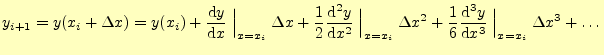
![\includegraphics[keepaspectratio, scale=1.0]{figure/Euler.eps}](img77.png)

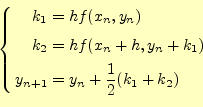
![\includegraphics[keepaspectratio, scale=1.0]{figure/RK2_1.eps}](img98.png)
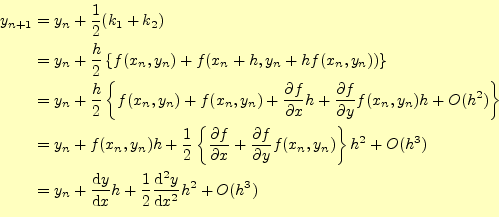
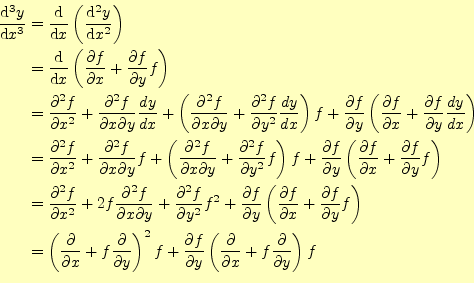
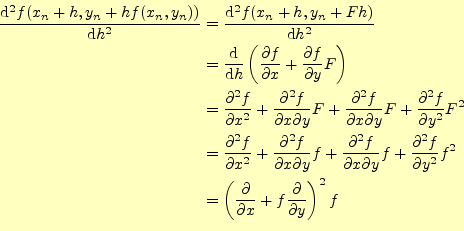

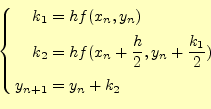
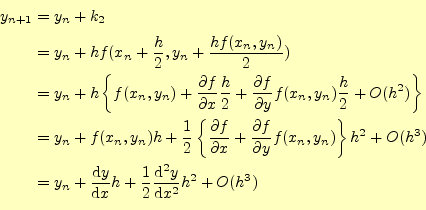
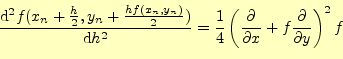
![\includegraphics[keepaspectratio, scale=1.0]{figure/RK2_2.eps}](img123.png)
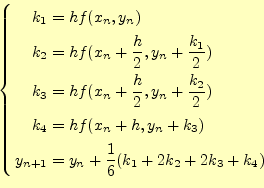
![\includegraphics[keepaspectratio, scale=1.0]{figure/RK4.eps}](img134.png)