理論から分かるように,スプライン補間を行うためには以下の2つの計算が必要である.
-4pt
- 各点での2次導関数の値
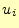 の計算
の計算
- 係数
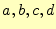 を求めて,補間の値の計算
を求めて,補間の値の計算
それぞれ,C言語の関数を作成することにする.それぞれの関数の作成方法について,以
下に述べる.
まず最初の関数で,標本点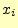 と
と から,
から,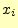 での2次導関数の値
での2次導関数の値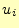 を計算する
プログラムである.この関数は,最初に1回呼び出すだけでよく,結果は補間値を計算す
る次の関数に渡す.この2次導関数の値を計算するプログラムは,独立した関数としてモ
ジュール化するのが常套手段である.そのほうが,プログラムが分かりやすくなり,メン
テナンスも容易である.
を計算する
プログラムである.この関数は,最初に1回呼び出すだけでよく,結果は補間値を計算す
る次の関数に渡す.この2次導関数の値を計算するプログラムは,独立した関数としてモ
ジュール化するのが常套手段である.そのほうが,プログラムが分かりやすくなり,メン
テナンスも容易である.
C言語の関数でこれを実現するための関数のプロトタイプ宣言は,
void spline_cal_u(int n, double x[], double y[], double u[]);
のようにすればよい.nは標本点の最大の番号である.標本点の番号は,0から
始まりnで終わる.配列x[]とy[]に標本のxとy座標の値を入
れる.配列u[]は計算された2次導関数の値が入る.
この関数での処理の内容は,
- 標本点での2次導関数の値
 が満たす連立方程式を作成する.
が満たす連立方程式を作成する.
- その連立方程式を解く.
である.要するに連立方程式を作り,そして解いているのである.解くべき連立方程式は,
次の通りである.
ただし,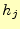 と
と は以下のとおり.
は以下のとおり.
この関数のフローチャートを図1に示す.この関数では,
連立方程式を解く必要がある.この連立方程式は,以下の特徴がある.
- 係数は,3重対角行列である.
- 対角成分は,ゼロにならない.
通常はLU分解,あるいは反復法で解くことになる.しかし,そのプログラムを書くのも面
倒なので,以前作成したピボット選択のないガウス・ジョルダンを使えばよい.連立方程
式により解かれた2次導関数の値は,配列u[]に入れられて呼び出し側に戻る.
連立方程式により計算される2次導関数の値は,
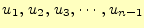 である.両端は自然境界条件で,
である.両端は自然境界条件で,
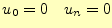 とする.こ
この関数では最後にその条件を配列をu[0]=0, u[n]=0とすることで実
現している.
とする.こ
この関数では最後にその条件を配列をu[0]=0, u[n]=0とすることで実
現している.
図 1:
2次導関数 を求める関数.
を求める関数.
|
|
2次導関数の値が分かったので,残りの処理は,その値を利用して任意の の補関値を求
めることである.スプライン補間は,3次の区分多項式で標本点の間を補完するのは今ま
で述べたとおりである.そのためには,標本点の座標と2次導関数の値,即ち
の補関値を求
めることである.スプライン補間は,3次の区分多項式で標本点の間を補完するのは今ま
で述べたとおりである.そのためには,標本点の座標と2次導関数の値,即ち
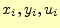 がわかれば計算できる.2次導関数の値
がわかれば計算できる.2次導関数の値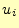 は予め,先の関数
spline_cal_u(n, x, y, u)で計算しておくものとする.
は予め,先の関数
spline_cal_u(n, x, y, u)で計算しておくものとする.
スプライン補間の計算に必要な
 から,補間点
から,補間点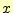 の値を求める関数を作
ろう.C 言語の関数でこれを実現するための関数のプロトタイプ宣言は,
の値を求める関数を作
ろう.C 言語の関数でこれを実現するための関数のプロトタイプ宣言は,
double spline(int n, double x[], double y[], double u[], double xx);
のようにすればよい.この関数の実引数xxに補関値を求めたい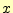 を入れるので
ある.そして,この関数の戻り値が
を入れるので
ある.そして,この関数の戻り値が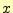 での補間値
での補間値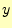 となる.
となる.
この関数の処理の内容は,
- 補間値を求める
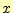 が,どの標本点の間にあるか探す.
が,どの標本点の間にあるか探す.
- 見つかった標本点の場所から,3次関数の係数を計算する.
- 3次関数から
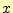 の時の値,
の時の値, を計算する.
を計算する.
である.ここで重要なことは, がある区間を探し,3次関数の係数を求めることである.
2次導関数と標本点の値から,それらの係数は
がある区間を探し,3次関数の係数を求めることである.
2次導関数と標本点の値から,それらの係数は
と計算できる.これらの係数から,補間の値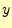 は
は
となる.
この関数のフローチャートを図2に示す.まず初めに, が存在す
る区間を2分探索により探している.これがわかれば,
が存在す
る区間を2分探索により探している.これがわかれば, を挟む場所の
を挟む場所の の値がわ
かる.そうすると,式(4)〜(7)を用いて,3次関数の補間式
の係数
の値がわ
かる.そうすると,式(4)〜(7)を用いて,3次関数の補間式
の係数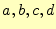 の値が計算できる.そして,式(8)から補間値
の値が計算できる.そして,式(8)から補間値 がわかる.
補間したい点
がわかる.
補間したい点 が変わる毎にspline(n, x, y, u, xx)を呼び出せばよいわけで
ある.
が変わる毎にspline(n, x, y, u, xx)を呼び出せばよいわけで
ある.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年11月28日
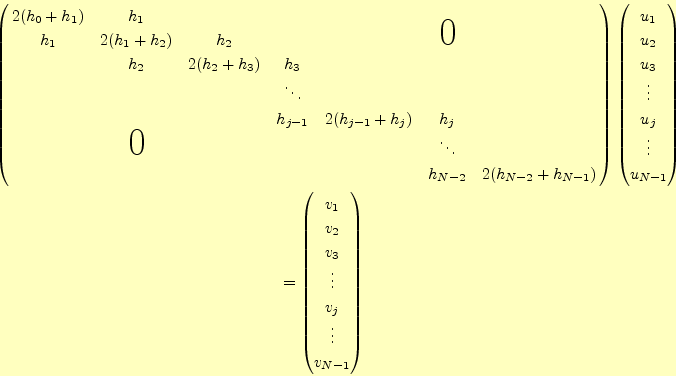
![$\displaystyle =6\left[\frac{y_{j+1}-y_j}{h_j} -\frac{y_j-y_{j-1}}{h_{j-1}}\right]$](img16.png)
![]() である.両端は自然境界条件で,
である.両端は自然境界条件で,
![]() とする.こ
この関数では最後にその条件を配列をu[0]=0, u[n]=0とすることで実
現している.
とする.こ
この関数では最後にその条件を配列をu[0]=0, u[n]=0とすることで実
現している.
![]() から,補間点
から,補間点![]() の値を求める関数を作
ろう.C 言語の関数でこれを実現するための関数のプロトタイプ宣言は,
の値を求める関数を作
ろう.C 言語の関数でこれを実現するための関数のプロトタイプ宣言は,![]() が存在す
る区間を2分探索により探している.これがわかれば,
が存在す
る区間を2分探索により探している.これがわかれば,![]() を挟む場所の
を挟む場所の![]() の値がわ
かる.そうすると,式(4)〜(7)を用いて,3次関数の補間式
の係数
の値がわ
かる.そうすると,式(4)〜(7)を用いて,3次関数の補間式
の係数![]() の値が計算できる.そして,式(8)から補間値
の値が計算できる.そして,式(8)から補間値![]() がわかる.
補間したい点
がわかる.
補間したい点![]() が変わる毎にspline(n, x, y, u, xx)を呼び出せばよいわけで
ある.
が変わる毎にspline(n, x, y, u, xx)を呼び出せばよいわけで
ある.